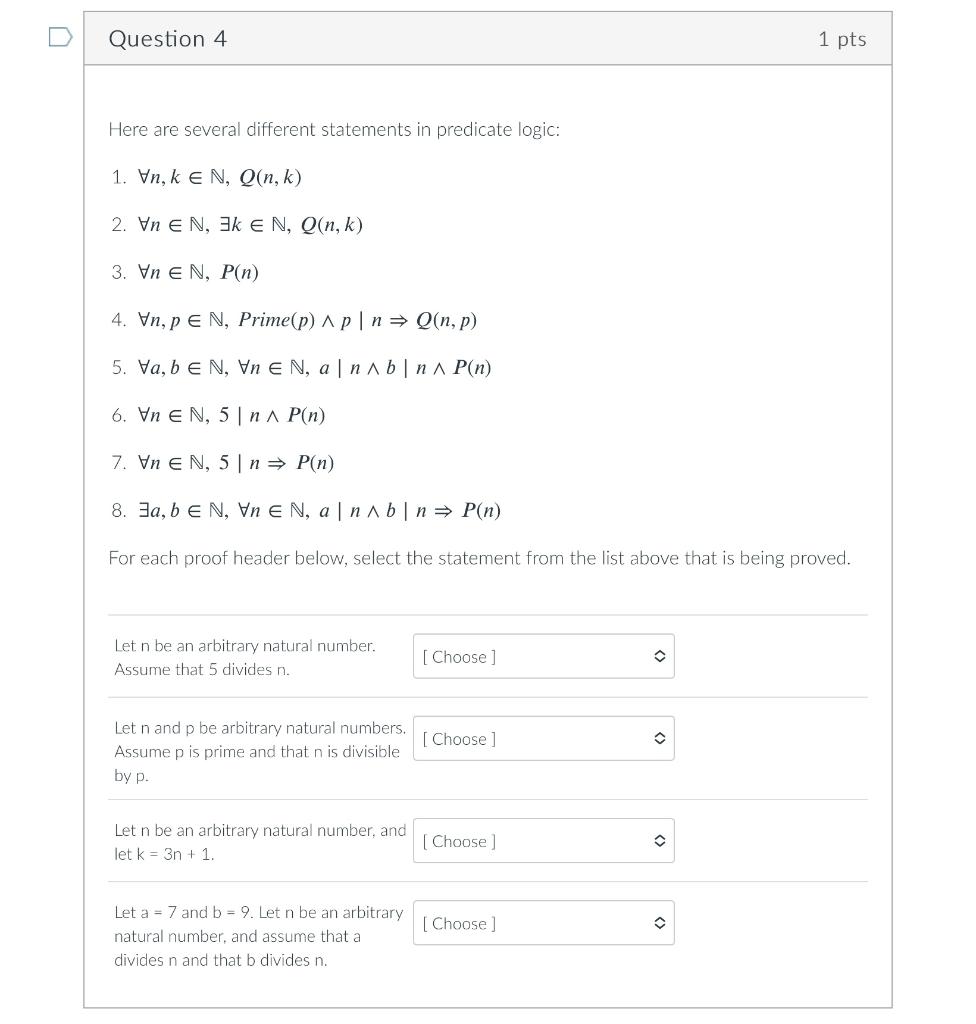
Here are several different statements in predicate logic: 1. n,kN,Q(n,k) 2. nN,kN,Q(n,k) 3. nN,P(n) 4. n,pN, Prime (p)pnQ(n,p) 5. a,bN,nN,anbnP(n) 6. nN,5nP(n) 7. nN,5nP(n) 8. a,bN,nN,anbnP(n) For each proof header below, select the statement from the list above that is being proved. Let n be an arbitrary natural number. Assume that 5 divides n. Let n and p be arbitrary natural numbers. Assume p is prime and that n is divisible by p. Let n be an arbitrary natural number, and let k=3n+1. Let a=7 and b=9. Let n be an arbitrary natural number, and assume that a divides n and that b divides n