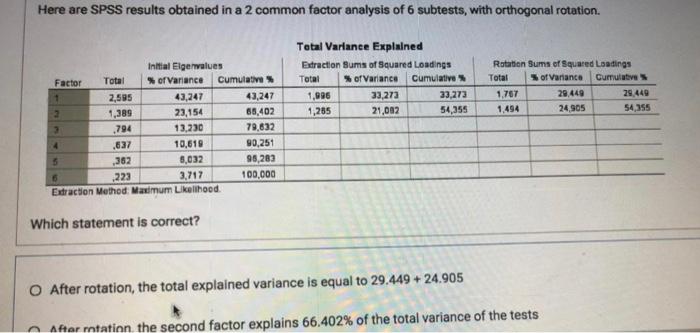
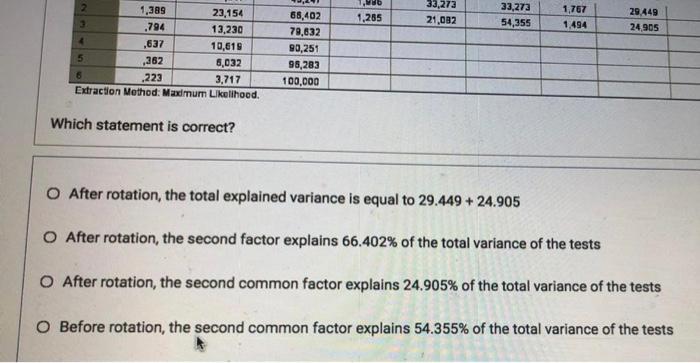
Here are SPSS results obtained in a 2 common factor analysis of 6 subtests, with orthogonal rotation Total Variance Explained Extraction Sums of Squared Loadings Total % of Variance Cumulative 1.996 33,273 33,272 1,265 21,082 54,355 Rotation Sums of Squared Leadings Total of Variance Cumulative 1,767 29.449 29.449 1.494 24,905 54 355 Initial Elger values Factor Total % of Variance Cumulative 1 2,595 43,247 43,247 a 1,389 23,154 68,402 3 ,794 13.230 79,832 4 .637 10,619 90.251 5 5,032 95,283 6 .223 3,717 100,000 Extraction Method: Maximum Likelihood ,362 Which statement is correct? O After rotation, the total explained variance is equal to 29.449 + 24.905 After mtation the second factor explains 66.402% of the total variance of the tests 1,285 33,273 21,092 33,273 54,355 1,767 1.494 29.449 24,905 1,389 23,154 3 .794 13,230 4 .637 10,619 5 ,262 8,032 6 ,223 3,717 Extraction Method: Maxdmurn Likelihood. 68,402 79,832 90,251 98,283 100,000 Which statement is correct? O After rotation, the total explained variance is equal to 29.449 + 24.905 After rotation, the second factor explains 66.402% of the total variance of the tests O After rotation, the second common factor explains 24.905% of the total variance of the tests Before rotation, the second common factor explains 54.355% of the total variance of the tests