Here is a question form the book 15e_An_Introduction_to_Management_Science_Quantitative_Approach : 6.5. I want to know how to build a model that generates the correct solution.

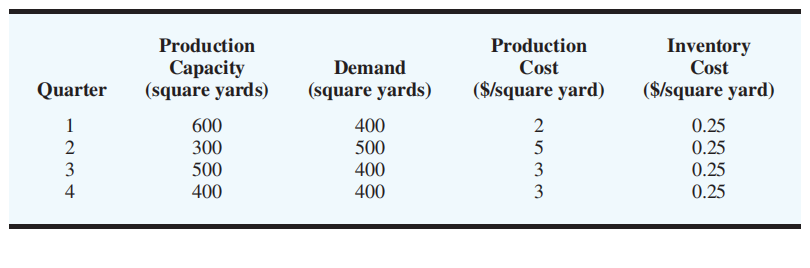
Contois Carpets is a small manufacturer of carpeting for home and office installations. Production capacity, demand, production cost per square yard, and inventory holding cost per square yard for the next four quarters are shown in Table 6.7. Note that production capacity, demand, and production costs vary by quarter, whereas the cost of carrying inventory from one quarter to the next is constant at $0.25 per yard. Contois wants to determine how many yards of carpeting to manufacture each quarter to minimize the total production and inventory cost for the four-quarter period. We begin by developing a network representation of the problem. First, we create four nodes corresponding to the production in each quarter and four nodes corresponding to the demand in each quarter. Each production node is connected by an outgoing arc to the demand node for the same period. The flow on the arc represents the number of square yards of carpet manufactured for the period. For each demand node, an outgoing arc represents the amount of inventory (square yards of carpet) carried over to the demand node for the next period. Figure 6.20 shows the network model. Note that nodes 14 represent the production for each quarter and that nodes 58 represent the demand for each quarter. The quarterly production capacities are shown in the left margin, and the quarterly demands are shown in the right margin. The objective is to determine a production scheduling and inventory policy that will minimize the total production and inventory cost for the four quarters. Constraints involve production capacity and demand in each quarter. As usual, a linear programming model can be developed from the network by establishing a constraint for each node and a variable for each arc.

Quarter 1 2 3 4 Production Capacity (square yards) 600 300 500 400 Demand (square yards) 400 500 400 400 Production Cost ($/square yard) 2 5 3 3 Inventory Cost ($/square yard) 0.25 0.25 0.25 0.25