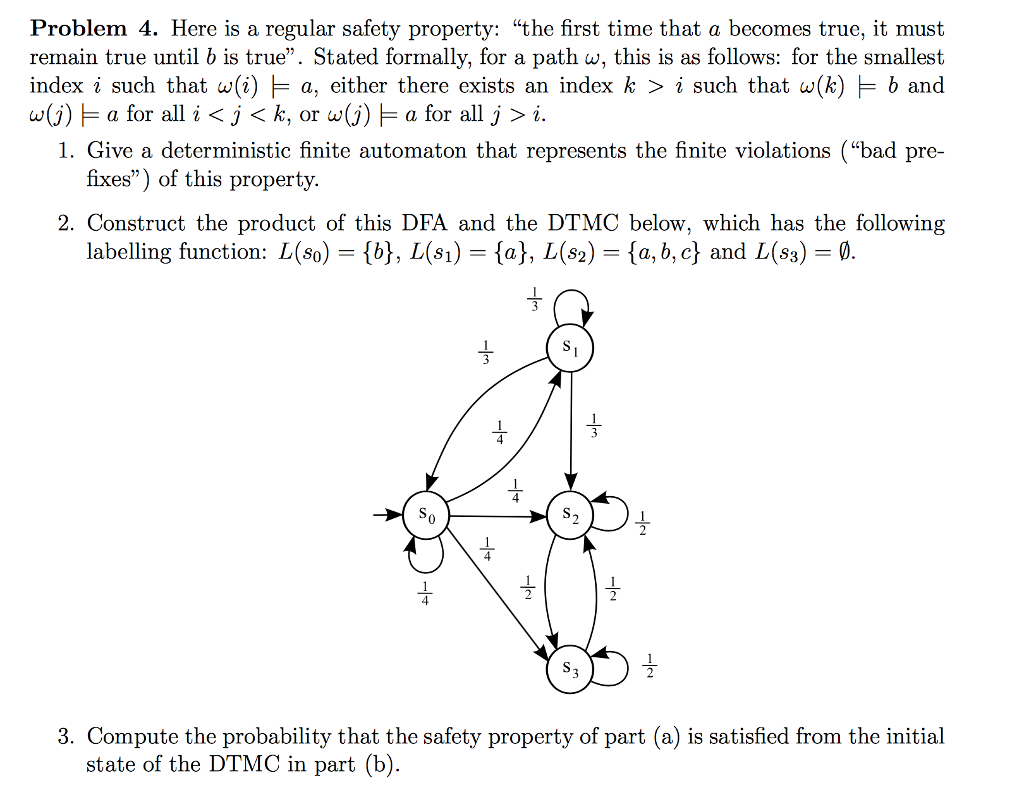
Here is a regular safety property: "the first time that a becomes true, it must remain true until b is true". Stated formally, for a path omega, this is as follows: for the smallest index i such that omega(i) |= a, either there exists an index k > i such that omega(k) |= b and omega(j) |= a for all i i. 1. Give a deterministic finite automaton that represents the finite violations ("bad pre-fixes") of this property. 2. Construct the product of this DFA and the DTMC below, which has the following labelling function: L(S_0) = {b}, L (s_1) = {a}, L (s_2) = {a, b, c} and L(s_3) = Theta. 3. Compute the probability that the safety property of part (a) is satisfied from the initial state of the DTMC in par (b). Here is a regular safety property: "the first time that a becomes true, it must remain true until b is true". Stated formally, for a path omega, this is as follows: for the smallest index i such that omega(i) |= a, either there exists an index k > i such that omega(k) |= b and omega(j) |= a for all i i. 1. Give a deterministic finite automaton that represents the finite violations ("bad pre-fixes") of this property. 2. Construct the product of this DFA and the DTMC below, which has the following labelling function: L(S_0) = {b}, L (s_1) = {a}, L (s_2) = {a, b, c} and L(s_3) = Theta. 3. Compute the probability that the safety property of part (a) is satisfied from the initial state of the DTMC in par (b)