here is question

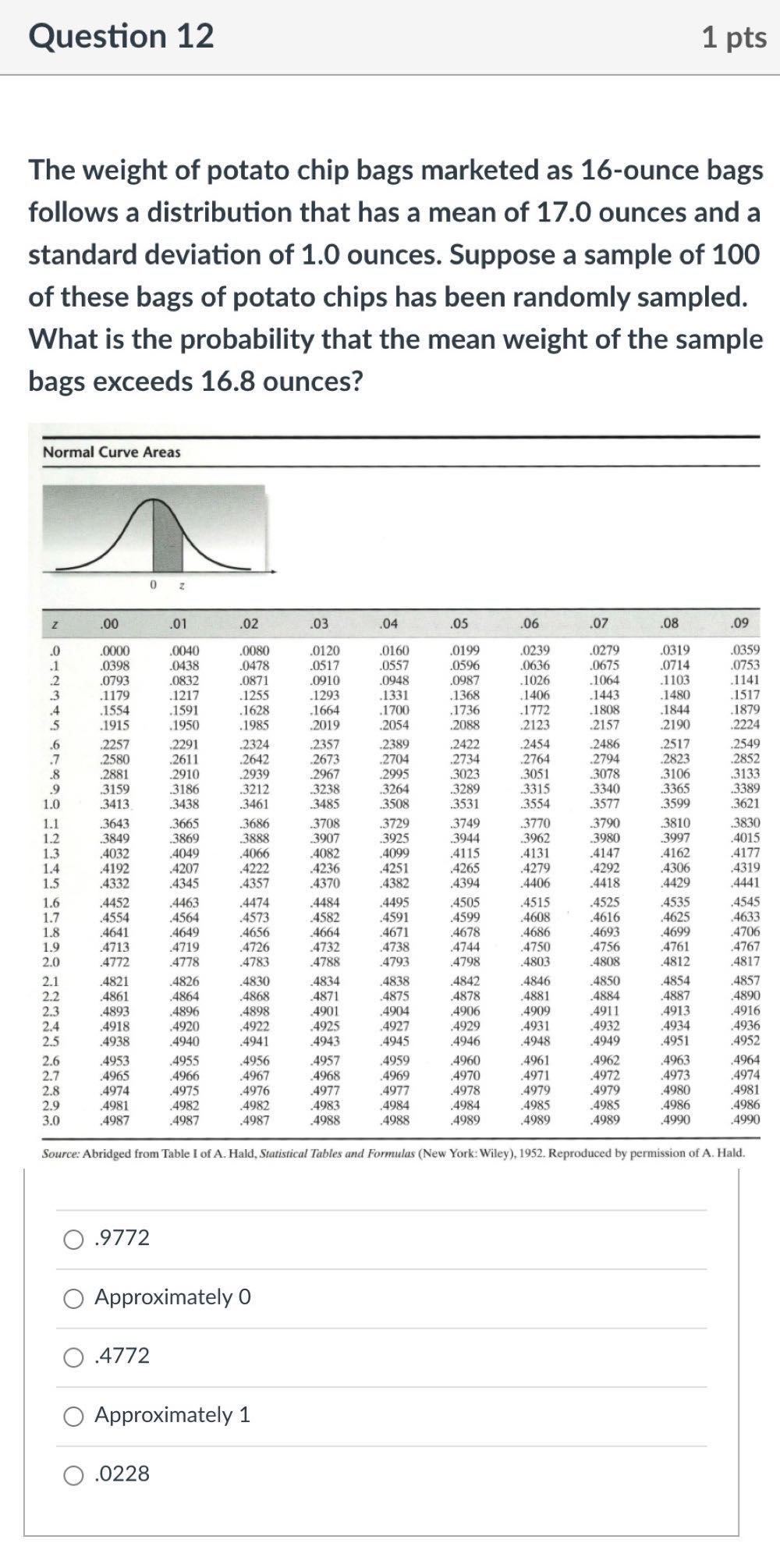
Question 6 2 pts A paint machine dispenses dye into paint cans to create different shades of paint. The amount of dye dispensed into a can is known to have a normal distribution witha mean of 5 milliliters (ml) and a standard deviation of .4 ml. Answer the following questions based on this information What proportion of the paint cans contain between 4.80 ml and 5.40 ml of the dye? O .1915 O .5328 O .3413 O.4758 O.1498 Question 7 2 pts A paint machine dispenses dye into paint cans to create different shades of paint. The amount of dye dispensed into a can is known to have a normal di mean of 5 milliliters (ml) and a standard deviation of .4 ml Answer the following questions based on this information Find the dye amount that represents the 9th percentile of the distribution O 4.464 ml ( 4.964 ml ( 4.836 ml 5.536 ml O 4.936 ml Question 8 1 pts The weight of potato chip bags marketed as 16-ounce bags follows a distribution that has a mean of 17.0 ounces and a standard deviation of 1.0 ounces. Suppose a sample of 100 of these bags of potato chips has been randomly sampled Which of the following statements about the Central Limit Theorem (CLT) is/are correct in the context of this problem? The CLT states that the population of potato chip weights will be approximately normally distributed. O All of these statements are correct The CLT states that the distribution for the 100 potato chip bag weights actually sampled will be approximately normally distributed. The CLT states that the distribution for the sample mean weights will be approximately normally distributed. Question 9 1 pts The weight of potato chip bags marketed as 16-ounce bags follows a distribution that has a mean of 17.0 ounces and a standard deviation of 1.0 ounces. Suppose a sample of 100 of these bags of potato chips has be What would be the mean and standard deviation of the sampling distribution for the sample mean weights? O mean - 1.7 ounces, standard deviation = ,10 ounces mean = 17 ounces, standard deviation = 1 ounce O mean = 17 ounces, standard deviation = 1 ounce O mean - 17 ounces, standard deviation - ,10 ounces Question 10 1 pts For a probability distribution to be valid, which of the following rules are true? O There are no rules. Probabilities can be anything and they can sum to any value. O Probabilities must all be between O and 1 and must sum to 1 Probabilities must all be between O and 1 but can sum to any value at all. O Probabilities can be any numbers but must sum to 1 Question 11 1 pts A friend has brought you a data set (because that's what friends do) and asked you to determine if it is approximately normally distributed. You analyze the data and find: 1. The histogram and the stem-and-leaf display both look kind of normally distributed. 2. An Empirical analysis indicates that 66% of the data fall within one standard deviation of the mean, 96% fall within two standard deviations of the mean and 99% fall within three standard deviations of the mean. 3. The normal probability plot looks extremely straight. 4. When you divided IQR by the standard deviation, you get the value 1.295 Do you believe the data is normally distributed? Yes! All four techniques yield results that are indicative of a normal distribution. Not sure. The results are split. Some of the techniques indicate a normal distribution while others indicate a non-normal No. none of the techniques yield results that are indicative of a normal distribution.Question 12 1 pts The weight of potato chip bags marketed as 16-ounce bags follows a distribution that has a mean of 17.0 ounces and a standard deviation of 1.0 ounces. Suppose a sample of 100 of these bags of potato chips has been randomly sampled. What is the probability that the mean weight of the sample bags exceeds 16.8 ounces? Normal Curve Areas Z 00 .01 .02 03 .04 05 06 07 08 09 .0000 .0040 .0080 .0120 .0398 .0160 .0438 .0199 0239 .0478 .0517 .0279 .0319 .0557 0832 .0596 0636 .0675 .1179 .0871 1217 .1255 .0948 .0714 .1026 .1591 .1331 .1368 1103 .1664 .1700 .1406 .1141 .1443 .1480 .1985 .1736 .2019 .1772 .2054 .1808 .2088 .1844 .2123 .1879 2291 .2324 .2157 .2190 .2580 .2611 .2357 .2389 .2642 .2673 .2422 .2454 .2704 .2734 2517 .2881 2910 .2939 .2995 .2764 .2794 2823 .2852 .3159 1.0 .3212 3023 .3413 3238 .3264 .3051 .3078 .3106 .3315 .3133 .3438 .3461 .3289 .3365 1.1 .3643 .3554 3599 1.2 3849 .3686 3621 1.3 .3888 .3708 .3729 .3749 4032 .3925 .3770 404 .3944 3790 .3810 .3830 1.4 4066 .4192 .4082 .4099 3980 3997 4015 1.5 .4207 .4131 4332 4345 4357 4236 .4251 .4265 .4162 4177 .4370 .4382 .4279 4306 .4319 1.6 .4406 4418 4429 .4452 .4463 4441 1.7 .4474 .4564 .4505 .4515 1.8 .4554 .4495 .4641 .4649 .4573 .4582 4656 .4591 4535 4664 .4599 .4608 1.9 4719 .4671 4678 4616 4625 4633 .4686 4699 4706 2.0 4772 4732 4778 4783 4738 4788 .4744 4793 4750 .4798 4756 .4803 4761 4767 2.1 4826 4812 4817 2.2 4821 4808 .4838 4842 2.3 4861 4864 4871 4896 4875 4878 4854 .4857 .4898 .4881 4901 4904 4884 4887 .4890 2.4 2.5 4918 4920 .4922 .4906 4909 .4927 4911 4913 4916 4938 .4925 4929 4931 4943 4945 4932 4946 .4934 .4936 2.6 4949 4953 4951 4952 2.7 2.8 4965 4956 4957 .4959 4967 4960 4963 4974 4968 4969 4962 4964 2.9 .4975 .4976 .4970 4971 .4977 .4978 .4972 4973 .4979 .4974 .4981 4982 4980 3.0 4987 4983 .4987 4984 .4987 4984 4981 4988 4985 .4988 .4989 4986 4986 .4990 4990 Source: Abridged from Table I of A. Hald, Statistical Tables and Formulas (New York: Wiley), 1952. Reproduced by permission of A. Hald. O .9772 O Approximately 0 O .4772 O Approximately 1 O .0228