here is the chapter description

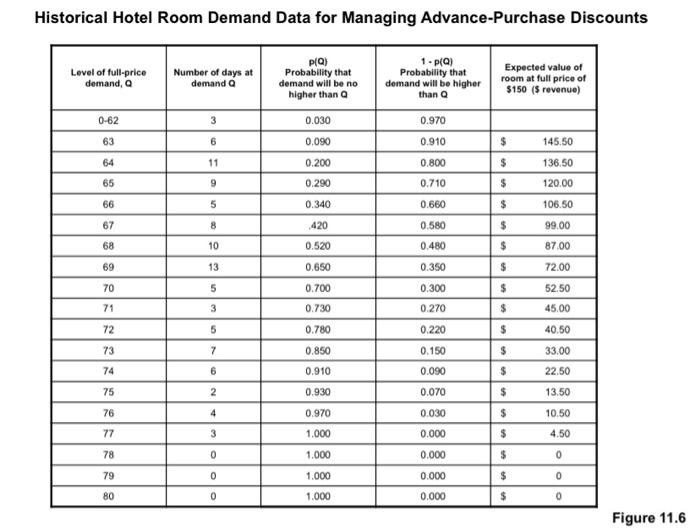
2. Consider again the chapter's description of the eighty-room hotel and the table in Figure 11.6. (a) Using the information in Figure 11.6, determine the maximum number of advance- purchase discounts to allow for the Monday in question if the discount price were $125 rather than $100. (b) Given your answer to Part (a), explain the direction of the difference between the maximum number of $125 advance-purchase discounts and the maximum number of $100 advance-purchase discounts. Historical Hotel Room Demand Data for Managing Advance-Purchase Discounts Level of full-price demand, a Number of days at demanda PIQ) Probability that demand will be no higher than a 1 .pa) Probability that demand will be higher than a Expected value of room at full price of $150 (5 revenue) 0-62 3 0.030 63 6 0.090 $ 145.50 64 11 0.970 0.910 0.800 0.710 0.660 0.200 0.290 $ 136.50 120.00 65 9 $ 66 5 0.340 $ 106.50 67 8 420 0.580 $ 99.00 68 10 0.520 0.480 $ 87.00 69 13 0.650 0.350 $ 72.00 70 5 0.700 $ 52.50 0,300 0.270 71 3 0.730 $ 45.00 72 5 0.780 $ 40.50 0.220 0.150 73 7 0.850 $ 33.00 74 6 0.910 0.090 $ 22.50 75 2 0.930 0.070 $ 13.50 76 4 0.970 0.030 $ 10.50 77 3 $ 4.50 1.000 1.000 78 0 $ 0 0.000 0.000 0.000 0.000 79 0 $ 0 1.000 1.000 80 0 $ 0 Figure 11.6 Using Probabilistic Historical Information The key to using probabilistic historical information to make pricing decision is the concept of expected value. We saw in Chapter 3 how the expected value of a variable - the average value of that variable in the long run could be useful in assessing a product's VTC. This important concept can also play a role in price segmentation. As mentioned in Chapter 1.revenue management is a set of price-setting techniques that are increasingly used to enhance profitability in service industries. Work in revenue management has led to the development of methods by which information that is relatively casy for a business to obtain can be used to calculate the expected value of a product's revenue - the product's expected revenue. These expected revenues can be very helpful in guiding decisions regarding advance-purchase discounts To illustrate revenue management methods, let's say that a bold with chrooms is trying to determine how many rooms on a particular upcoming Monday should be kept for sale at the full price of $150 and how many should be offered at anhance purchase discount price of S100 To estimate the number of full-price business customers who are likely to book rooms on that day, the hotel's management would construct a table showing the number of rooms that were booked on, say, one hundred similar Mondays when ne discounts were available (see Figure 116). The first column of the table is cach possible level of demand for full-price rooms (which we will call Q). The second column is the number of days that each level of Occurred. The third column is the cumulative proportion of days that full price demand was equal to or lower than Q This proportion represents the probability that full-price bookings occurred at demund Q or below, and will be referred to as plo) Note how this cumulative proportion information makes possible the calculation of expected revenues. IfpXO) for any row is the probability that full-price demand will be equal to or lower than , then! - PIQ) is the probability that full-price demand will be higher than Q (see the fourth column of the table). If fall-price demand is higher than then the room represented by the following row will be purchased at full price. Since we now know the probability that this following-row room will be purchased at full price fie, 1-POJ.we can calculate the expected dollar revenue of this room. It is equal to the full price times the probability that the room will be purchased at full price (see the fifth column of the table For example, there were eighty-five Mondays out of one hundred when seventy-three or fewer full-price rooms were booked, so there is a 0.85 probability that full-price Monday demand will be equal to or less than seventy-three rooms. That means that there is a 0.15 probability that demand will be greater than seventy-three rooms and the seventy-fourth room would be purchased at full price. Thus, the expected revenue of the seventy-fourth room equals $150 0.15, or $22.50 To understand how this expected revenue information can be useful, consider the hotel management's question concerning how many rooms should be offered at an advance purchase discount price of $100. If the expected revenue of a room is greater than $100, then revenue will be lost in the long run) by selling the room for only $100. However, if a room's expected revenue is less than 100, then selling that room at an advance purchase discount of Stoo will in the long run) lead to increased revenue. Thus, based on the data shown in the fifth column of the Figure 11.6 table, the sixty-seventh room and all remaining rooms (fourteen in all) can profitably be offered at the $100 advance-purchase discount This table of cumulative proportions could also help the hotel's management consider other options. For example, the managers may have found that an advance-purchase discount price of $100 is still too high to attract many of the leisure customers in the hotel's market, and are thus considering lowering it to say. 575. The information in the fifth celamin of the Figure 116 table would tell them that it would not be profitable to sell the sixty-seventh and sixty-eighthrooms for $75 because they both have expected revenues higher than $75. Thus, an advance purchase discount price of $75 could be offered profitably for a maximum of only twelve rooms. It certainly makes sense that the deeper the advance purchase discount, the smaller would be the het of discounts available to be old 2. Consider again the chapter's description of the eighty-room hotel and the table in Figure 11.6. (a) Using the information in Figure 11.6, determine the maximum number of advance- purchase discounts to allow for the Monday in question if the discount price were $125 rather than $100. (b) Given your answer to Part (a), explain the direction of the difference between the maximum number of $125 advance-purchase discounts and the maximum number of $100 advance-purchase discounts. Historical Hotel Room Demand Data for Managing Advance-Purchase Discounts Level of full-price demand, a Number of days at demanda PIQ) Probability that demand will be no higher than a 1 .pa) Probability that demand will be higher than a Expected value of room at full price of $150 (5 revenue) 0-62 3 0.030 63 6 0.090 $ 145.50 64 11 0.970 0.910 0.800 0.710 0.660 0.200 0.290 $ 136.50 120.00 65 9 $ 66 5 0.340 $ 106.50 67 8 420 0.580 $ 99.00 68 10 0.520 0.480 $ 87.00 69 13 0.650 0.350 $ 72.00 70 5 0.700 $ 52.50 0,300 0.270 71 3 0.730 $ 45.00 72 5 0.780 $ 40.50 0.220 0.150 73 7 0.850 $ 33.00 74 6 0.910 0.090 $ 22.50 75 2 0.930 0.070 $ 13.50 76 4 0.970 0.030 $ 10.50 77 3 $ 4.50 1.000 1.000 78 0 $ 0 0.000 0.000 0.000 0.000 79 0 $ 0 1.000 1.000 80 0 $ 0 Figure 11.6 Using Probabilistic Historical Information The key to using probabilistic historical information to make pricing decision is the concept of expected value. We saw in Chapter 3 how the expected value of a variable - the average value of that variable in the long run could be useful in assessing a product's VTC. This important concept can also play a role in price segmentation. As mentioned in Chapter 1.revenue management is a set of price-setting techniques that are increasingly used to enhance profitability in service industries. Work in revenue management has led to the development of methods by which information that is relatively casy for a business to obtain can be used to calculate the expected value of a product's revenue - the product's expected revenue. These expected revenues can be very helpful in guiding decisions regarding advance-purchase discounts To illustrate revenue management methods, let's say that a bold with chrooms is trying to determine how many rooms on a particular upcoming Monday should be kept for sale at the full price of $150 and how many should be offered at anhance purchase discount price of S100 To estimate the number of full-price business customers who are likely to book rooms on that day, the hotel's management would construct a table showing the number of rooms that were booked on, say, one hundred similar Mondays when ne discounts were available (see Figure 116). The first column of the table is cach possible level of demand for full-price rooms (which we will call Q). The second column is the number of days that each level of Occurred. The third column is the cumulative proportion of days that full price demand was equal to or lower than Q This proportion represents the probability that full-price bookings occurred at demund Q or below, and will be referred to as plo) Note how this cumulative proportion information makes possible the calculation of expected revenues. IfpXO) for any row is the probability that full-price demand will be equal to or lower than , then! - PIQ) is the probability that full-price demand will be higher than Q (see the fourth column of the table). If fall-price demand is higher than then the room represented by the following row will be purchased at full price. Since we now know the probability that this following-row room will be purchased at full price fie, 1-POJ.we can calculate the expected dollar revenue of this room. It is equal to the full price times the probability that the room will be purchased at full price (see the fifth column of the table For example, there were eighty-five Mondays out of one hundred when seventy-three or fewer full-price rooms were booked, so there is a 0.85 probability that full-price Monday demand will be equal to or less than seventy-three rooms. That means that there is a 0.15 probability that demand will be greater than seventy-three rooms and the seventy-fourth room would be purchased at full price. Thus, the expected revenue of the seventy-fourth room equals $150 0.15, or $22.50 To understand how this expected revenue information can be useful, consider the hotel management's question concerning how many rooms should be offered at an advance purchase discount price of $100. If the expected revenue of a room is greater than $100, then revenue will be lost in the long run) by selling the room for only $100. However, if a room's expected revenue is less than 100, then selling that room at an advance purchase discount of Stoo will in the long run) lead to increased revenue. Thus, based on the data shown in the fifth column of the Figure 11.6 table, the sixty-seventh room and all remaining rooms (fourteen in all) can profitably be offered at the $100 advance-purchase discount This table of cumulative proportions could also help the hotel's management consider other options. For example, the managers may have found that an advance-purchase discount price of $100 is still too high to attract many of the leisure customers in the hotel's market, and are thus considering lowering it to say. 575. The information in the fifth celamin of the Figure 116 table would tell them that it would not be profitable to sell the sixty-seventh and sixty-eighthrooms for $75 because they both have expected revenues higher than $75. Thus, an advance purchase discount price of $75 could be offered profitably for a maximum of only twelve rooms. It certainly makes sense that the deeper the advance purchase discount, the smaller would be the het of discounts available to be old