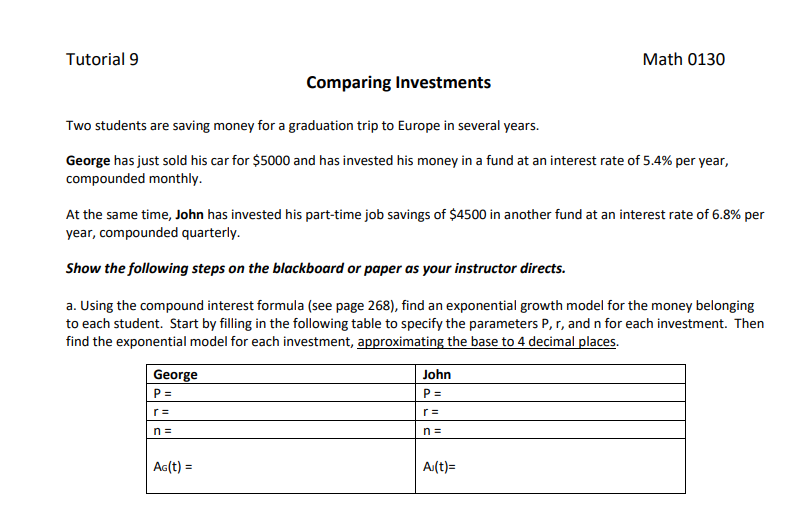
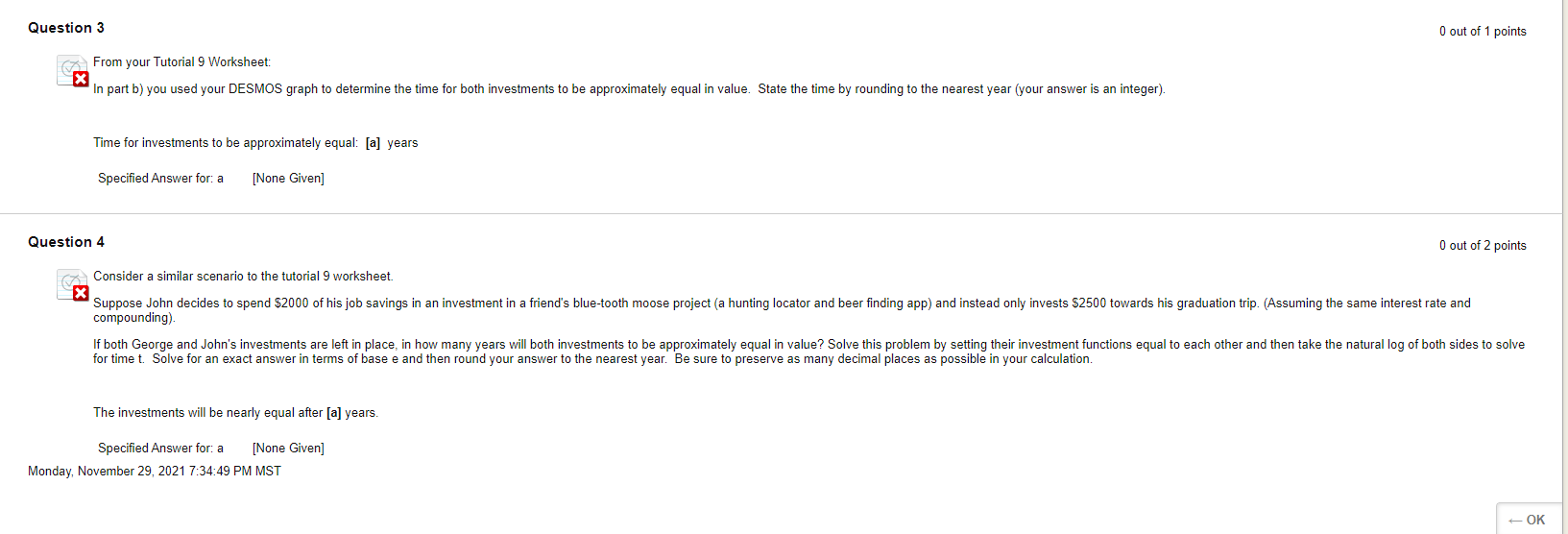
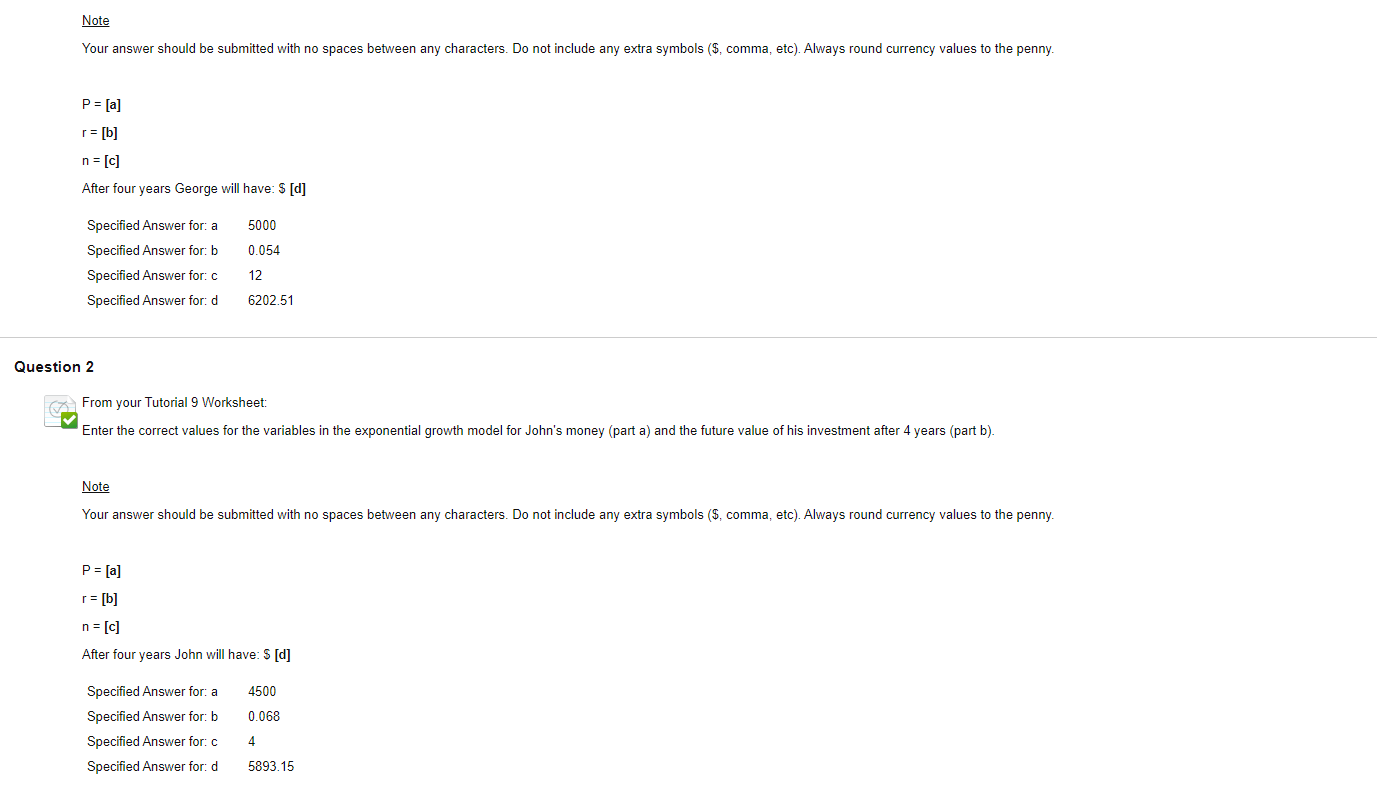
Question: Here is the problem context, I already figure out the equation, I just couldn't solve for these two. Tutorial 9 Math 0130 Comparing Investments Two
Here is the problem context, I already figure out the equation, I just couldn't solve for these two.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


