Here is the problem transcribed:

' Considering the expression (1/(sqrt(1+ax)))-sqrt(1-x) where a belongs to the set of rational numbers and a does not equal 0. The binomial expansion of this expression, in ascending powers of x, as far as the term in x^2, is 4bx+bx^2, where b belongs to the set of all rational numbers.

PART A: Find the value of a and the value of b.

PART B: State the restriction which must be placed on x for this expansion to be valid.'

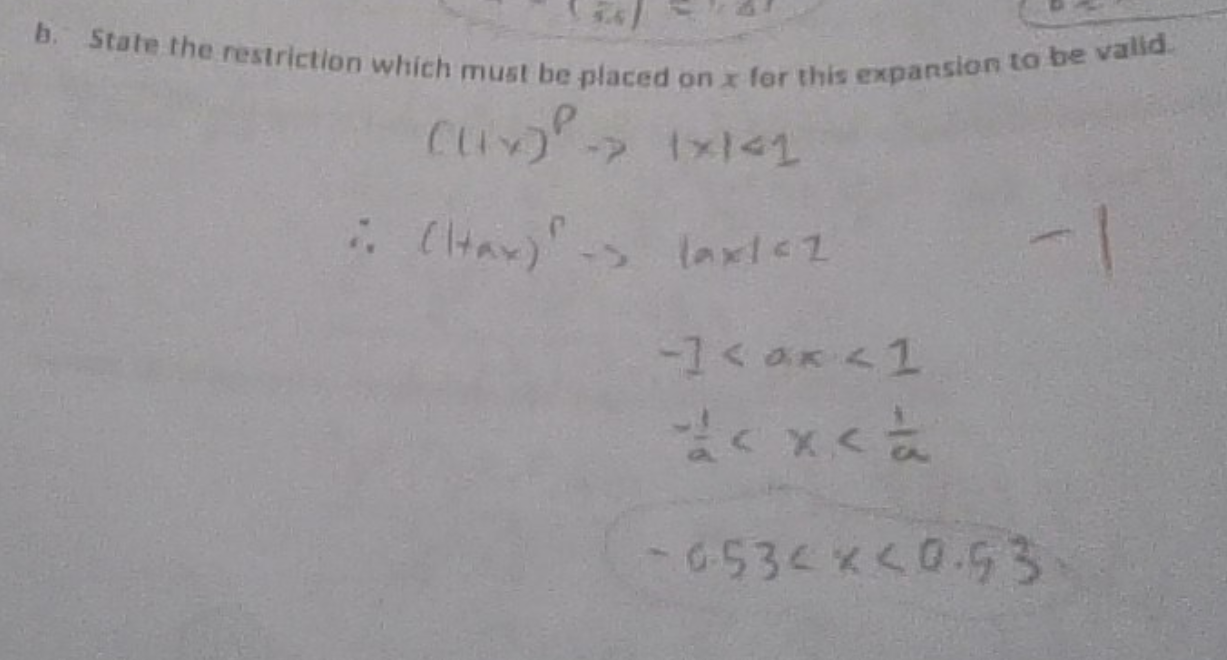
7 4. (7) Consider the expression VI+ax - V1 - x where a E Q, a # 0. The binomial expansion of this expression, in ascending powers of x, as far as the term in x is 4bx + bx, where b E Q. a. Find the value of a and the value of b. (ltax ) 2 = 1+ - JIx lc ! S ( K CH. 5 ) ( cock-.)... ( K+8.5) M8 . ( x) 2 - 5 Equate binarial based on each C: ( 3 #.5 ) Jax- JX = 46X Sale for a ed b (2415 ) Jax - VY = byb. State the restriction which must be placed on a for this expansion to be valid (() - 1X141 ". ( Htax ) - laxl sz -1