Here is the question

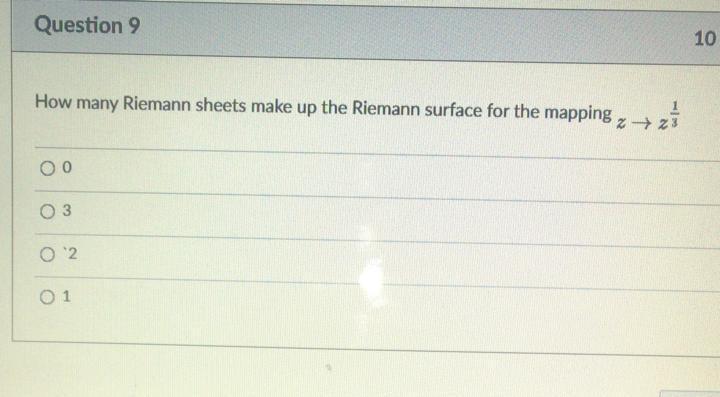
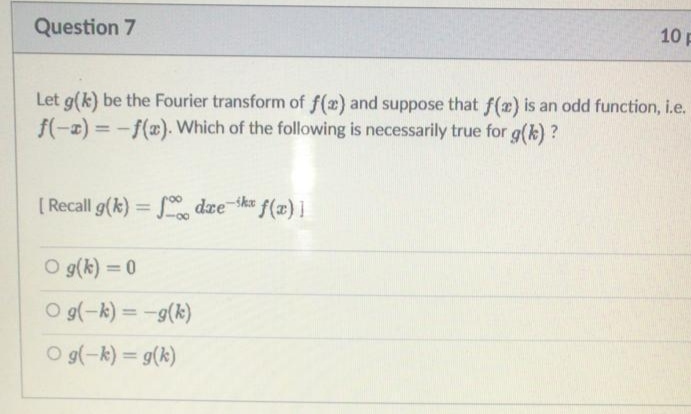
\fConsider the ODE dy/de = f(x, y), with y(0) = 0. Suppose that the second order Runge Kutta method is used to obtain the solution for y(x = 1), dividing the interval into N subintervals. Suppose that N is large and consider the error on y( = 1). By what factor does this error decrease when N is increased by a factor of 10? [ Recall that the 2nd order Runge Kutta method evaluates yit1 = yi + k2 + O((8x)), where k2 = ox f(x,, y:), k2 - 6x f(x; + 6x/2, y: + k1/2) ]. O 10000 100 10 1000Question 7 10 Let g(k) be the Fourier transform of f() and suppose that f() is an odd function, i.e. f(-x) = - f(z). Which of the following is necessarily true for g( k) ? [ Recall g(k) = Jo dre h f(x) ] O g(k) = 0 O g(-k) = -g(k) O g(-k) = g(k)