Here is the starter code:

/**
     * Given a 2D array of ints return the value of the
     * most valuable contiguous sub rectangle in the 2D array.
     * The sub rectangle must be at least 1 by 1.
     *

pre: mat != null, mat.length > 0, mat[0].length > 0,
     * mat is a rectangular matrix.
     *

post: return the value of the most valuable contiguous sub rectangle
     * in city.

     * @param city The 2D array of ints representing the value of
     * each block in a portion of a city.
     * @return return the value of the most valuable contiguous sub rectangle
     * in city.
     */
    public static int getValueOfMostValuablePlot(int[][] city) {
        // check preconditions
        if (city == null || city.length == 0 || city[0].length == 0
                || !isRectangular(city) ) {
            throw new IllegalArgumentException("Violation of precondition: " +
                    "getValueOfMostValuablePlot. The parameter may not be null," +
                    " must value at least one row and at least" +
                    " one column, and must be rectangular.");
        }
       
    }

Here is testers:

board = new char[][] { { '.', '.', '.', 'q' },
                { '.', '.', '.', '.' },
                { '.', '.', '.', '.' },
                { 'q', '.', '.', '.' } };
        expectedBool = false;
board = new char[][] { { 'q', '.', '.', '.', '.', '.', '.' },
                { '.', '.', '.', '.', 'q', '.', '.' },
                { '.', 'q', '.', '.', '.', '.', '.' },
                { '.', '.', '.', '.', '.', 'q', '.' },
                { '.', '.', 'q', '.', '.', '.', '.' },
                { '.', '.', '.', '.', '.', '.', 'q' },
                { '.', '.', '.', 'q', '.', '.', '.' } };
        expectedBool = true;
board = new char[][] {
                { 'q', '.', '.', '.', '.', '.', '.', '.', '.', '.' },
                { '.', '.', '.', '.', 'q', '.', '.', '.', '.', '.' },
                { '.', 'q', '.', '.', '.', '.', '.', '.', '.', '.' },
                { '.', '.', '.', '.', '.', 'q', '.', '.', '.', '.' },
                { '.', '.', 'q', '.', '.', '.', '.', '.', '.', '.' },
                { '.', '.', '.', '.', '.', '.', 'q', '.', '.', '.' },
                { '.', '.', '.', 'q', '.', '.', '.', '.', '.', '.' },
                { '.', '.', '.', '.', '.', '.', '.', '.', '.', '.' },
                { '.', '.', '.', '.', '.', '.', '.', '.', '.', '.' },
                { '.', '.', '.', '.', '.', '.', '.', '.', 'q', '.' }, };
        expectedBool = false;

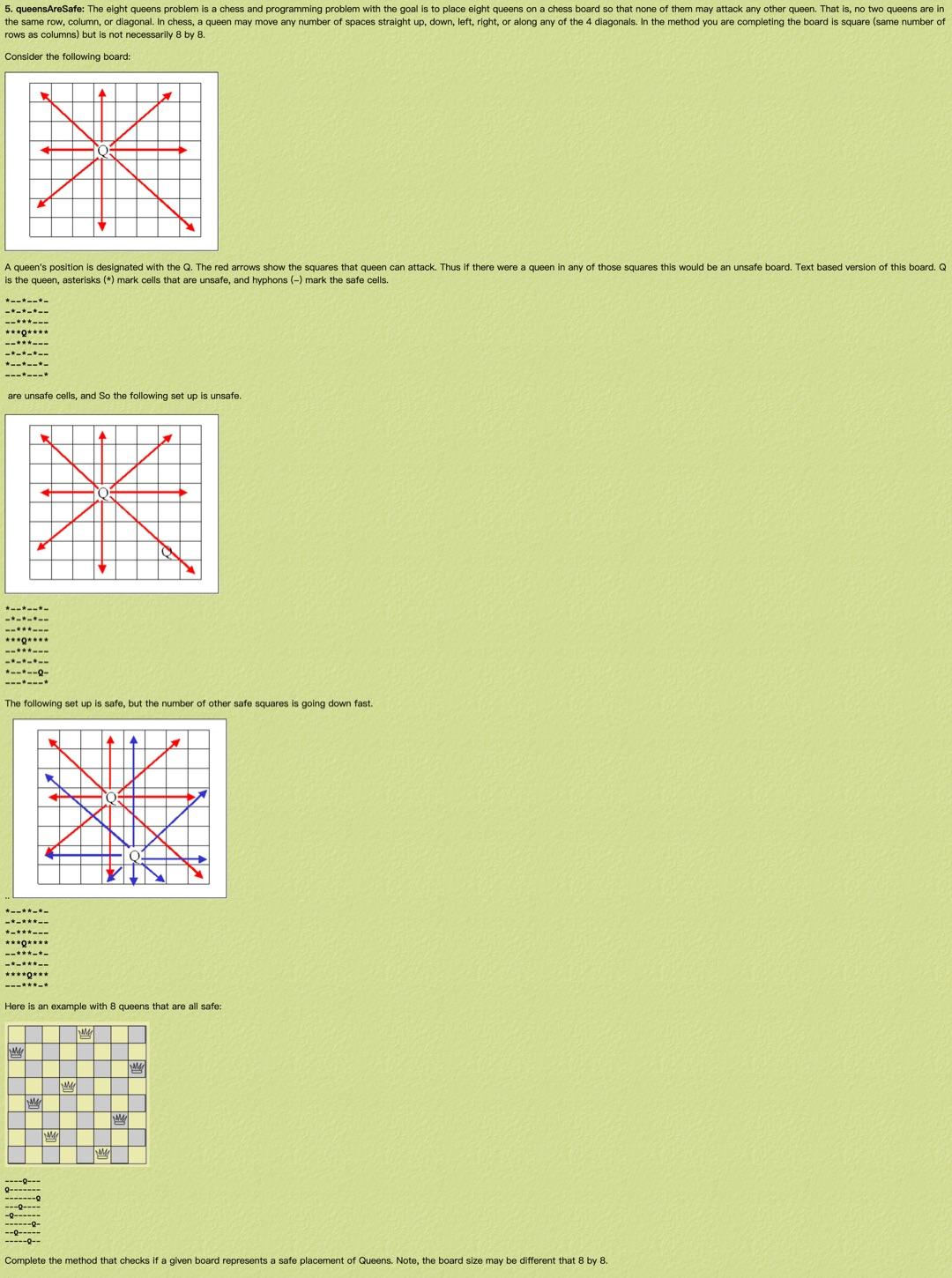
5. queensAreSafe: The eight queens problem is a chess and programming problem with the goal is to place eight queens on a chess board so that none of them may attack any other queen. That is, no two queens are in the same row, column, or diagonal. In chess, a queen may move any number of spaces straight up, down, left, right, or along any of the 4 diagonals. In the method you are completing the board is square (same number of rows as columns) but is not necessarily 8 by 8. Consider the following board: A queen's position is designated with the Q. The red arrows show the squares that queen can attack. Thus if there were a queen in any of those squares this would be an unsafe board. Text based version of this board. Q is the queen, asterisks (*) mark cells that are unsafe, and hyphons (-) mark the safe cells. are unsafe cells, and So the following set up is unsafe. *-*-*- ******* --***--- 1111110 The following set up is safe, but the number of other safe squares is going down fast. ******* Here is an example with queens that are all safe: M Q------ ------ 1181111 --- ------0- --8--- -----8- M X M W Complete the method that checks if a given board represents a safe placement of Queens. Note, the board size may be different that 8 by 8.