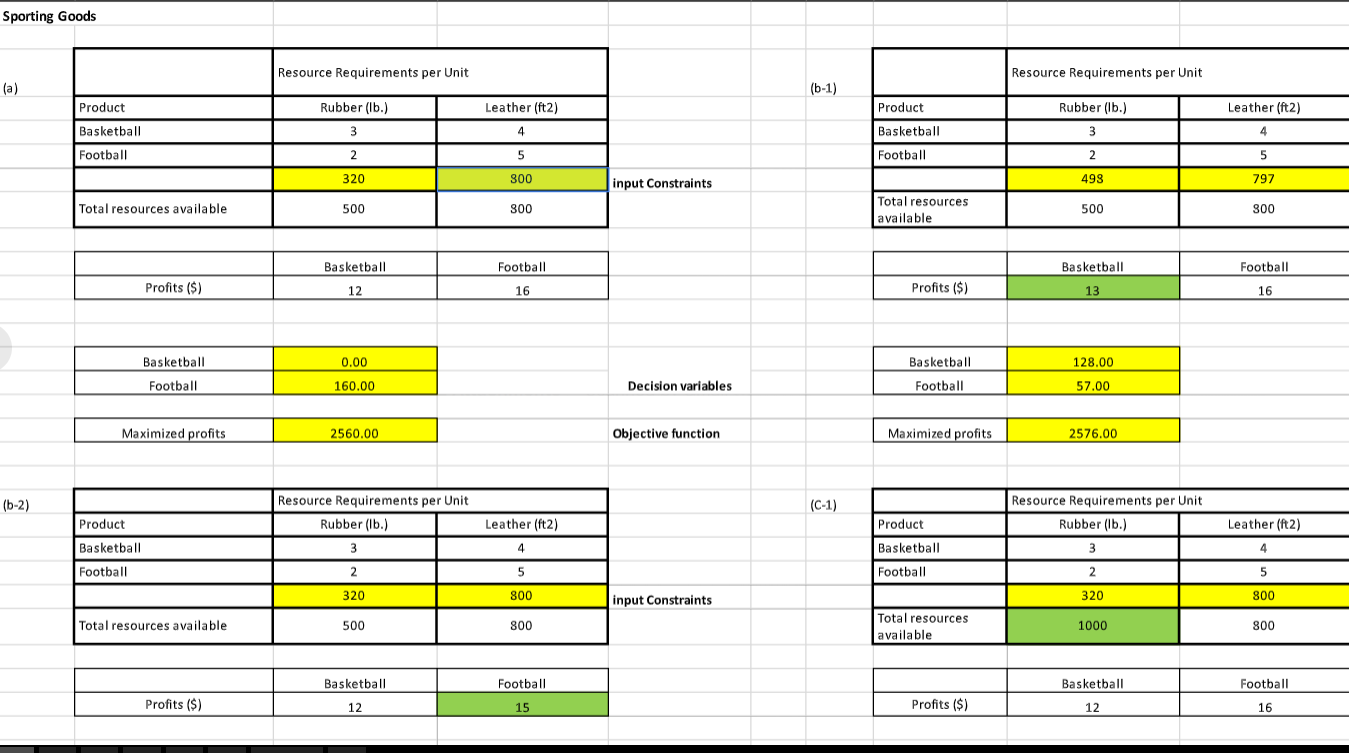
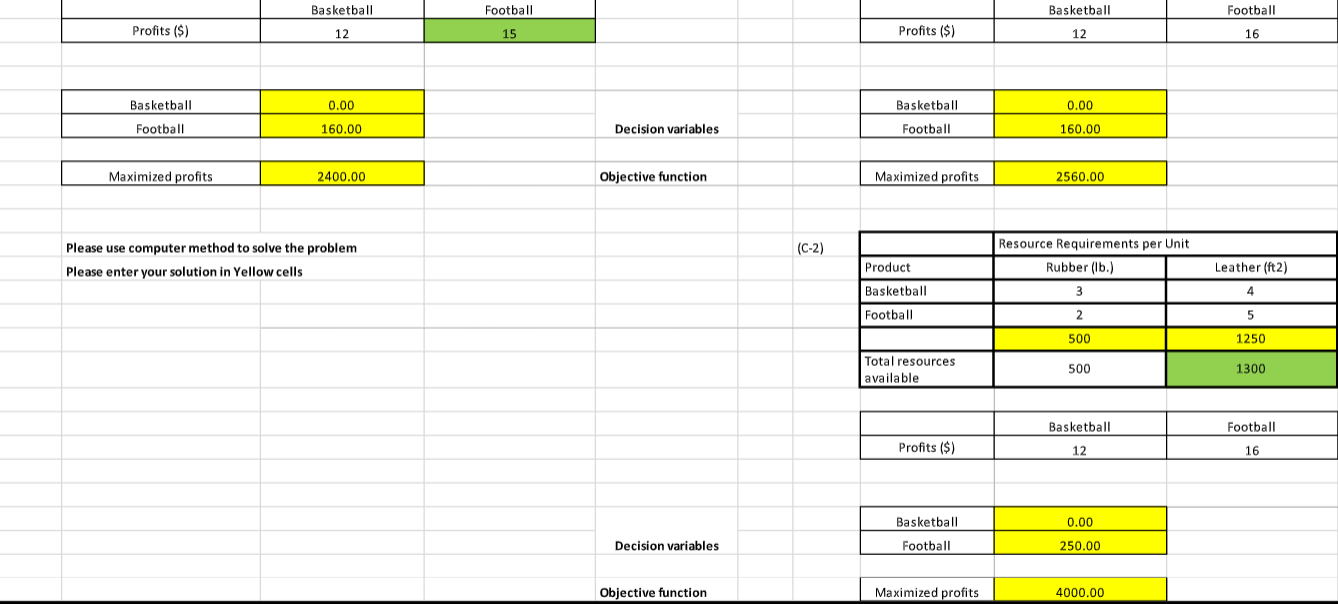
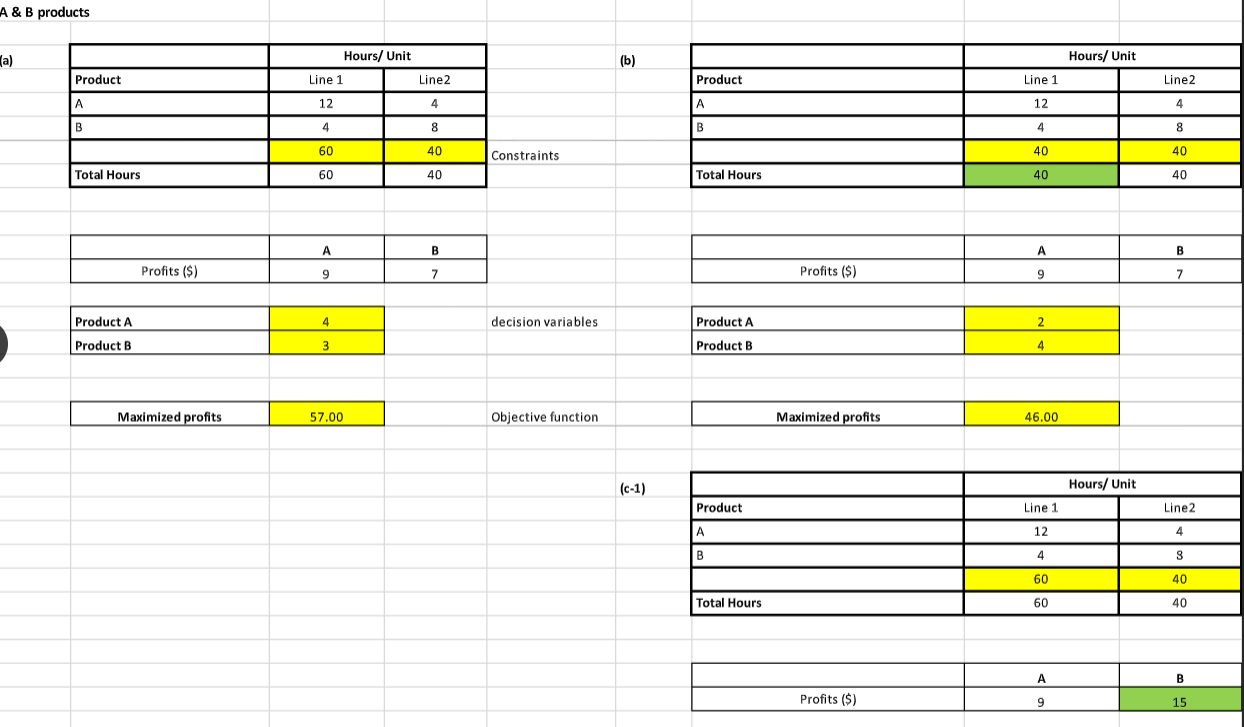
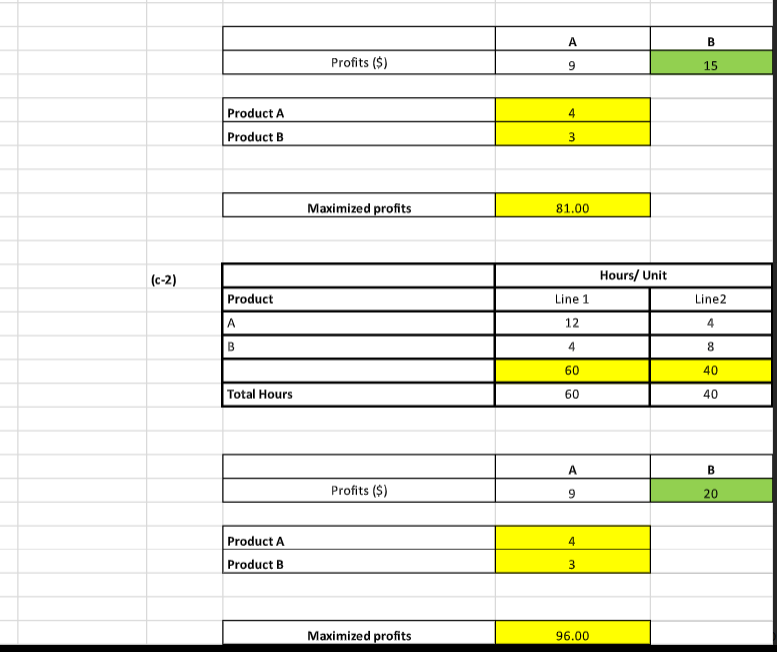
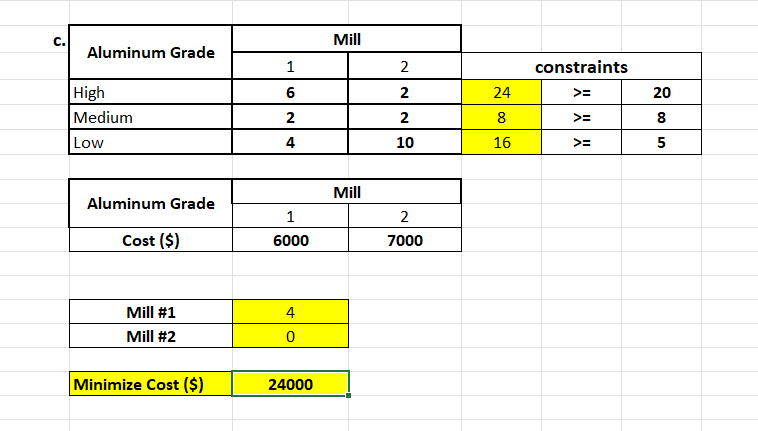
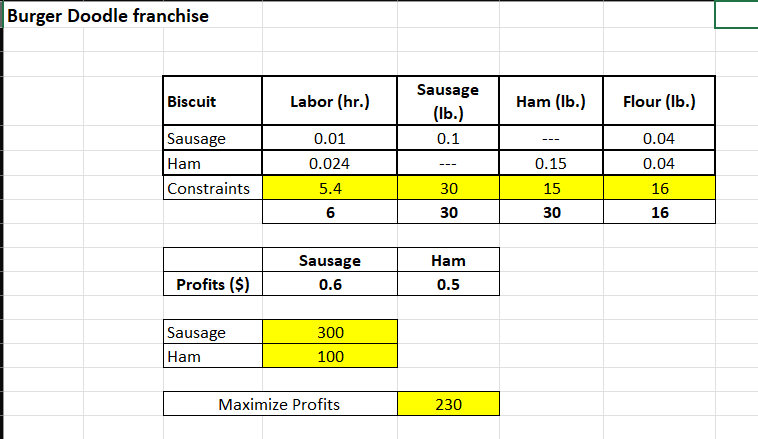
HEY NEED THIS URGENTLY CAN ANYONE PLEASE MAKE A SENSITIVITY ANALYSIS REPORT FOR THIS AND CAN ANYON ETELL ME HOW TO DO IT ASWELL IN STEPS.

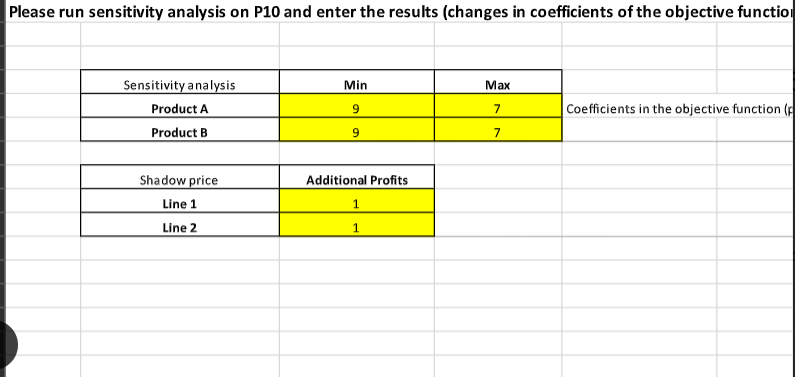
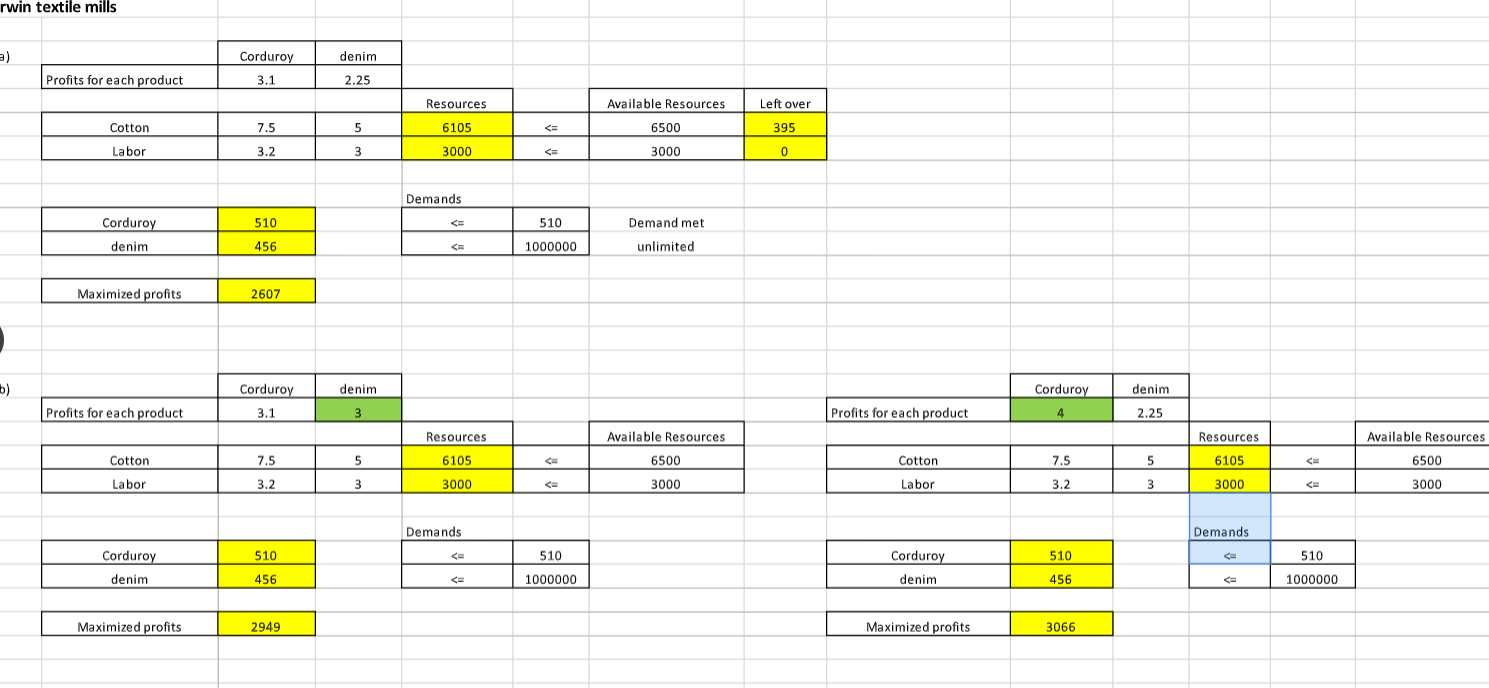
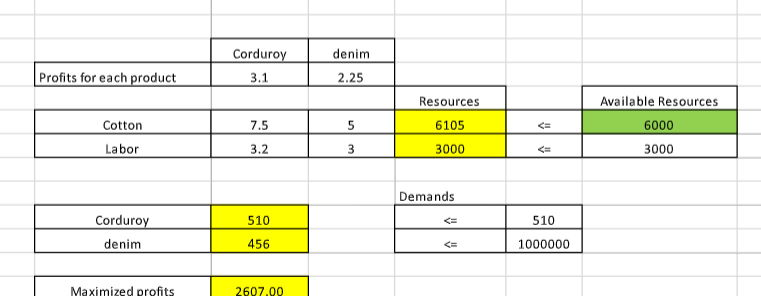
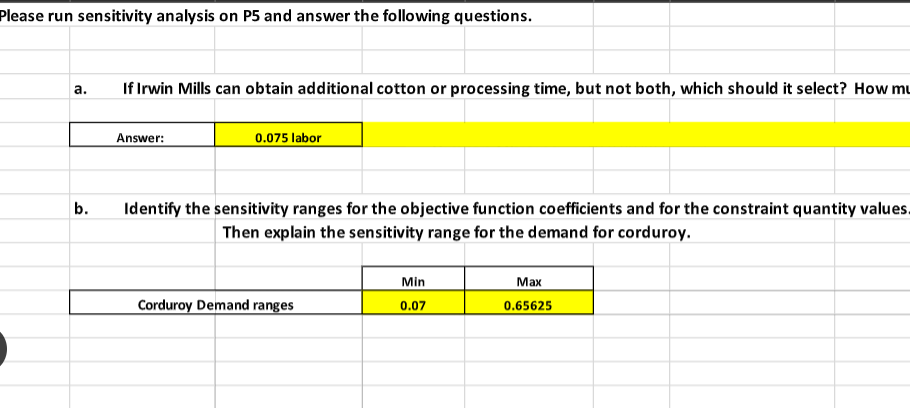
S A \& B products \begin{tabular}{|l|c|c|} \hline & \multicolumn{2}{|c|}{ Hours/ Unit } \\ \hline Product & Line 1 & Line2 \\ \hline A & 12 & 4 \\ \hline B & 4 & 8 \\ \hline & 60 & 40 \\ \hline Total Hours & 60 & 40 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits (\$) & 9 & 7 \\ \hline \end{tabular} Note: SUMPRODUCT(Col1, Col2) is a easier way to multiply two rows or two columns Standard Linear Programming: Maximixe Subject to 9A+7B 12A+4B=0 B>=0 A \& B products (a) \begin{tabular}{|l|c|c|} \hline & \multicolumn{2}{|c|}{ Hours/ Unit } \\ \hline Product & Line 1 & Line2 \\ \hline A & 12 & 4 \\ \hline B & 4 & 8 \\ \hline & 60 & 40 \\ \hline Total Hours & 60 & 40 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits (\$) & 9 & 7 \\ \hline \end{tabular} (b) \begin{tabular}{|l|c|c|} \hline & \multicolumn{2}{|c|}{ Hours/ Unit } \\ \hline Product & Line 1 & Line2 \\ \hline A & 12 & 4 \\ \hline B & 4 & 8 \\ \hline & 40 & 40 \\ \hline Total Hours & 40 & 40 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits ($) & 9 & 7 \\ \hline \end{tabular} \begin{tabular}{|l|c|} \hline Product A & 2 \\ \hline Product B & 4 \\ \hline & \\ \hline Maximized profits & \\ \hline \end{tabular} (c-1) \begin{tabular}{|l|c|c|} \hline & \multicolumn{2}{|c|}{ Hours/ Unit } \\ \hline Product & Line 1 & Line2 \\ \hline A & 12 & 4 \\ \hline B & 4 & 3 \\ \hline & 60 & 40 \\ \hline Total Hours & 60 & 40 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits ($) & 9 & 15 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits (\$) & 9 & 15 \\ \hline \end{tabular} \begin{tabular}{|l|c|} \hline Product A & 4 \\ \hline Product B & 3 \\ \hline \end{tabular} (c-2) \begin{tabular}{|l|c|} \hline Product A & 4 \\ \hline Product B & 3 \\ \hline \end{tabular} Maximized profits 96.00 Please run sensitivity analysis on P10 and enter the results (changes in coefficients of the objective functio rwin textile mills b. Identify the sensitivity ranges for the objective function coefficients and for the constraint quantity values Then explain the sensitivity range for the demand for corduroy. c. \begin{tabular}{|l|c|c|c|c|c|} \hline \multirow{2}{*}{ Aluminum Grade } & \multicolumn{3}{|c|}{ Mill } & \multicolumn{2}{c|}{} \\ \cline { 2 - 5 } & 1 & 2 & \multicolumn{3}{|c|}{ constraints } \\ \hline High & 6 & 2 & 24 & >= & 20 \\ \hline Medium & 2 & 2 & 8 & >= & 8 \\ \hline Low & 4 & 10 & 16 & >= & 5 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline \multirow{2}{*}{ Aluminum Grade } & \multicolumn{2}{|c|}{ Mill } \\ \cline { 2 - 3 } & 1 & 2 \\ \hline Cost ($) & 6000 & 7000 \\ \hline \end{tabular} \begin{tabular}{|l|l|} \hline Mill \#1 & 4 \\ \hline Mill \#2 & 0 \\ \hline \end{tabular} \begin{tabular}{|l|l|} \hline Minimize Cost (\$) & 24000 \\ \hline \end{tabular} Burger Doodle franchise \begin{tabular}{|c|c|c|} \hline & Sausage & Ham \\ \hline Profits (\$) & 0.6 & 0.5 \\ \hline \end{tabular} \begin{tabular}{|l|l|} \hline Sausage & 300 \\ \hline Ham & 100 \\ \hline \end{tabular} \begin{tabular}{|l|c|} \hline Maximize Profits & 230 \\ \hline \end{tabular} S A \& B products \begin{tabular}{|l|c|c|} \hline & \multicolumn{2}{|c|}{ Hours/ Unit } \\ \hline Product & Line 1 & Line2 \\ \hline A & 12 & 4 \\ \hline B & 4 & 8 \\ \hline & 60 & 40 \\ \hline Total Hours & 60 & 40 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits (\$) & 9 & 7 \\ \hline \end{tabular} Note: SUMPRODUCT(Col1, Col2) is a easier way to multiply two rows or two columns Standard Linear Programming: Maximixe Subject to 9A+7B 12A+4B=0 B>=0 A \& B products (a) \begin{tabular}{|l|c|c|} \hline & \multicolumn{2}{|c|}{ Hours/ Unit } \\ \hline Product & Line 1 & Line2 \\ \hline A & 12 & 4 \\ \hline B & 4 & 8 \\ \hline & 60 & 40 \\ \hline Total Hours & 60 & 40 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits (\$) & 9 & 7 \\ \hline \end{tabular} (b) \begin{tabular}{|l|c|c|} \hline & \multicolumn{2}{|c|}{ Hours/ Unit } \\ \hline Product & Line 1 & Line2 \\ \hline A & 12 & 4 \\ \hline B & 4 & 8 \\ \hline & 40 & 40 \\ \hline Total Hours & 40 & 40 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits ($) & 9 & 7 \\ \hline \end{tabular} \begin{tabular}{|l|c|} \hline Product A & 2 \\ \hline Product B & 4 \\ \hline & \\ \hline Maximized profits & \\ \hline \end{tabular} (c-1) \begin{tabular}{|l|c|c|} \hline & \multicolumn{2}{|c|}{ Hours/ Unit } \\ \hline Product & Line 1 & Line2 \\ \hline A & 12 & 4 \\ \hline B & 4 & 3 \\ \hline & 60 & 40 \\ \hline Total Hours & 60 & 40 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits ($) & 9 & 15 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline & A & B \\ \hline Profits (\$) & 9 & 15 \\ \hline \end{tabular} \begin{tabular}{|l|c|} \hline Product A & 4 \\ \hline Product B & 3 \\ \hline \end{tabular} (c-2) \begin{tabular}{|l|c|} \hline Product A & 4 \\ \hline Product B & 3 \\ \hline \end{tabular} Maximized profits 96.00 Please run sensitivity analysis on P10 and enter the results (changes in coefficients of the objective functio rwin textile mills b. Identify the sensitivity ranges for the objective function coefficients and for the constraint quantity values Then explain the sensitivity range for the demand for corduroy. c. \begin{tabular}{|l|c|c|c|c|c|} \hline \multirow{2}{*}{ Aluminum Grade } & \multicolumn{3}{|c|}{ Mill } & \multicolumn{2}{c|}{} \\ \cline { 2 - 5 } & 1 & 2 & \multicolumn{3}{|c|}{ constraints } \\ \hline High & 6 & 2 & 24 & >= & 20 \\ \hline Medium & 2 & 2 & 8 & >= & 8 \\ \hline Low & 4 & 10 & 16 & >= & 5 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|} \hline \multirow{2}{*}{ Aluminum Grade } & \multicolumn{2}{|c|}{ Mill } \\ \cline { 2 - 3 } & 1 & 2 \\ \hline Cost ($) & 6000 & 7000 \\ \hline \end{tabular} \begin{tabular}{|l|l|} \hline Mill \#1 & 4 \\ \hline Mill \#2 & 0 \\ \hline \end{tabular} \begin{tabular}{|l|l|} \hline Minimize Cost (\$) & 24000 \\ \hline \end{tabular} Burger Doodle franchise \begin{tabular}{|c|c|c|} \hline & Sausage & Ham \\ \hline Profits (\$) & 0.6 & 0.5 \\ \hline \end{tabular} \begin{tabular}{|l|l|} \hline Sausage & 300 \\ \hline Ham & 100 \\ \hline \end{tabular} \begin{tabular}{|l|c|} \hline Maximize Profits & 230 \\ \hline \end{tabular}