Hi, can I get some help, please?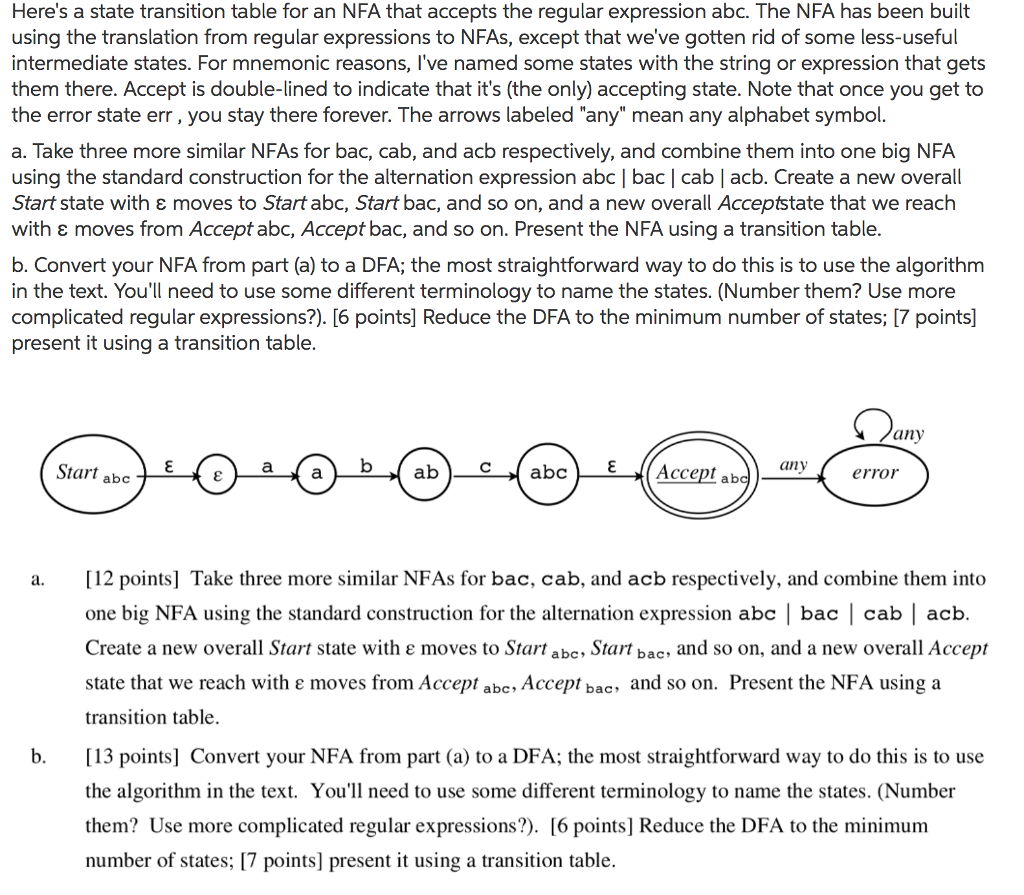

Here's a state transition table for an NFA that accepts the regular expression abc. The NFA has been built using the translation from regular expressions to NFAs, except that we've gotten rid of some less-useful intermediate states. For mnemonic reasons, I've named some states with the string or expression that gets them there. Accept is double-lined to indicate that it's (the only) accepting state. Note that once you get to the error state err, you stay there forever. The arrows labeled "any" mean any alphabet symbol a. Take three more similar NFAs for bac, cab, and acb respectively, and combine them into one big NFA using the standard construction for the alternation expression abc | bac |cab |acb. Create a new overall Start state with moves to Start abc, Start bac, and so on, and a new overall Acceptstate that we reach with moves from Accept abc, Accept bac, and so on. Present the NFA using a transition table. b. Convert your NFA from part (a) to a DFA; the most straightforward way to do this is to use the algorithm in the text. You'll need to use some different terminology to name the states. (Number them? Use more complicated regular expressions?). [6 points] Reduce the DFA to the minimum number of states; [7 points] present it using a transition table. an Start abc abCabc any Accept error a.[12 points] Take three more similar NFAs for bac, cab, and acb respectively, and combine them into one big NFA using the standard construction for the alternation expression abc | bac cab | acb Create a new overall Start state with e moves to Startabc, Start bac, and so on, and a new overall Accept state that we reach with e moves from Accept abc, Accept bac, and so on. Present the NFA using a transition table. b.[13 points] Convert your NFA from part (a) to a DFA; the most straightforward way to do this is to use the algorithm in the text. You'll need to use some different terminology to name the states. (Number them? Use more complicated regular expressions?). [6 points] Reduce the DFA to the minimum number of states; [7 points] present it using a transition table