hi! can you help me do these questions please?

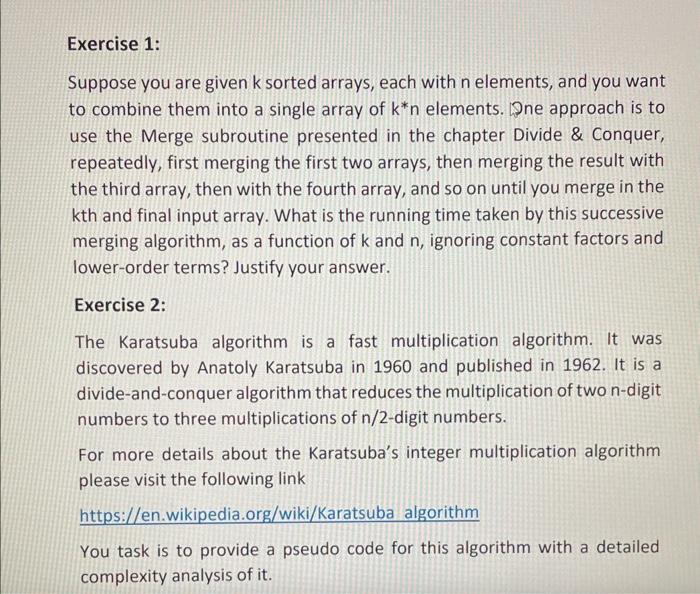
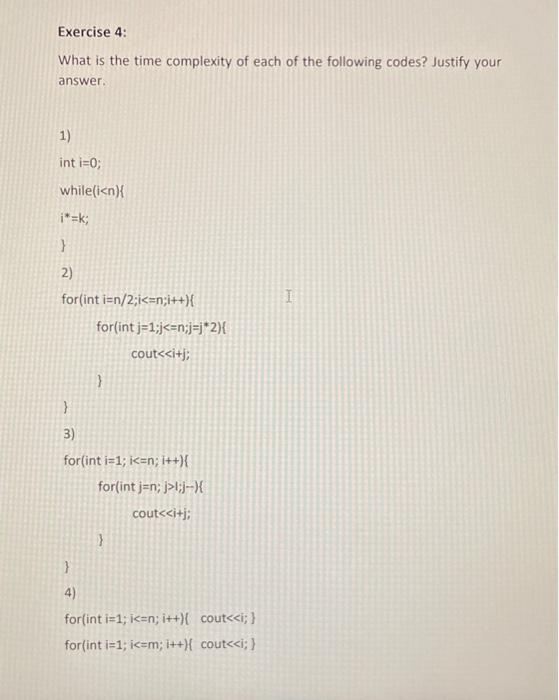
Exercise 1: Suppose you are given k sorted arrays, each with n elements, and you want to combine them into a single array of kn elements. One approach is to use the Merge subroutine presented in the chapter Divide \& Conquer, repeatedly, first merging the first two arrays, then merging the result with the third array, then with the fourth array, and so on until you merge in the k th and final input array. What is the running time taken by this successive merging algorithm, as a function of k and n, ignoring constant factors and lower-order terms? Justify your answer. Exercise 2: The Karatsuba algorithm is a fast multiplication algorithm. It was discovered by Anatoly Karatsuba in 1960 and published in 1962. It is a divide-and-conquer algorithm that reduces the multiplication of two n-digit numbers to three multiplications of n /2-digit numbers. For more details about the Karatsuba's integer multiplication algorithm please visit the following link https://en.wikipedia.org/wiki/Karatsuba algorithm You task is to provide a pseudo code for this algorithm with a detailed complexity analysis of it. Find g(n) such that f(n)=O(g(n)) Exercise 4: What is the time complexity of each of the following codes? Justify your answer. 1) int i=0 while (i1;j)cout