Question

1 Approved Answer

Posted on Oct 10, 2024

hi, could you help with this programming assignment and it is due tonight 11:45. One of the tutor already worked on the code, but I

hi, could you help with this programming assignment and it is due tonight 11:45. One of the tutor already worked on the code, but I could't run it. could you please check it and help me changed the file name to "Project2.m"

Here's the problem:

In this project, we will calculate the trajectories of a mini solar system consisting of the Sun, Mercury, Earth, and the Moon. The motion of celestial bodies is governed by Newtons second law of motion and gravity. The program SunEarthMoon.m on the class website simulates the orbits of the Sun, Earth, and the Moon. Modify this program to include the motion of Mercury as well. You need to research and code in the right mass/distance/velocity parameters for Mercury in order for this simulation to work.

For Programming Assignment #2:

Reformulate the system of second order ODEs into a system of first order ODEs, and solve

the system with the matlab function ode45.

Your program should take the same input arguments years and framerate. Your output should be

a plot depicting the orbits of the Moon and the Earth.

a plot depicting the orbits of the Earth, Mercury, and the Sun.

CLARIFICATION:

This programming assignment asks you to predict the motions of the given four objects interacting with each other gravitationally. Specifically, you are asked to produce *only* the following two plots:

1. orbit of the Moon relative to the Earth, which is a 3D plot;

2. orbits of the Earth, Sun and Mercury on xy plane, which is a 2D plot. They are equivalent to the orbits of the Earth and Mercury relative to the Sun on xy plane, as the Sun will roughly stay at the origin.

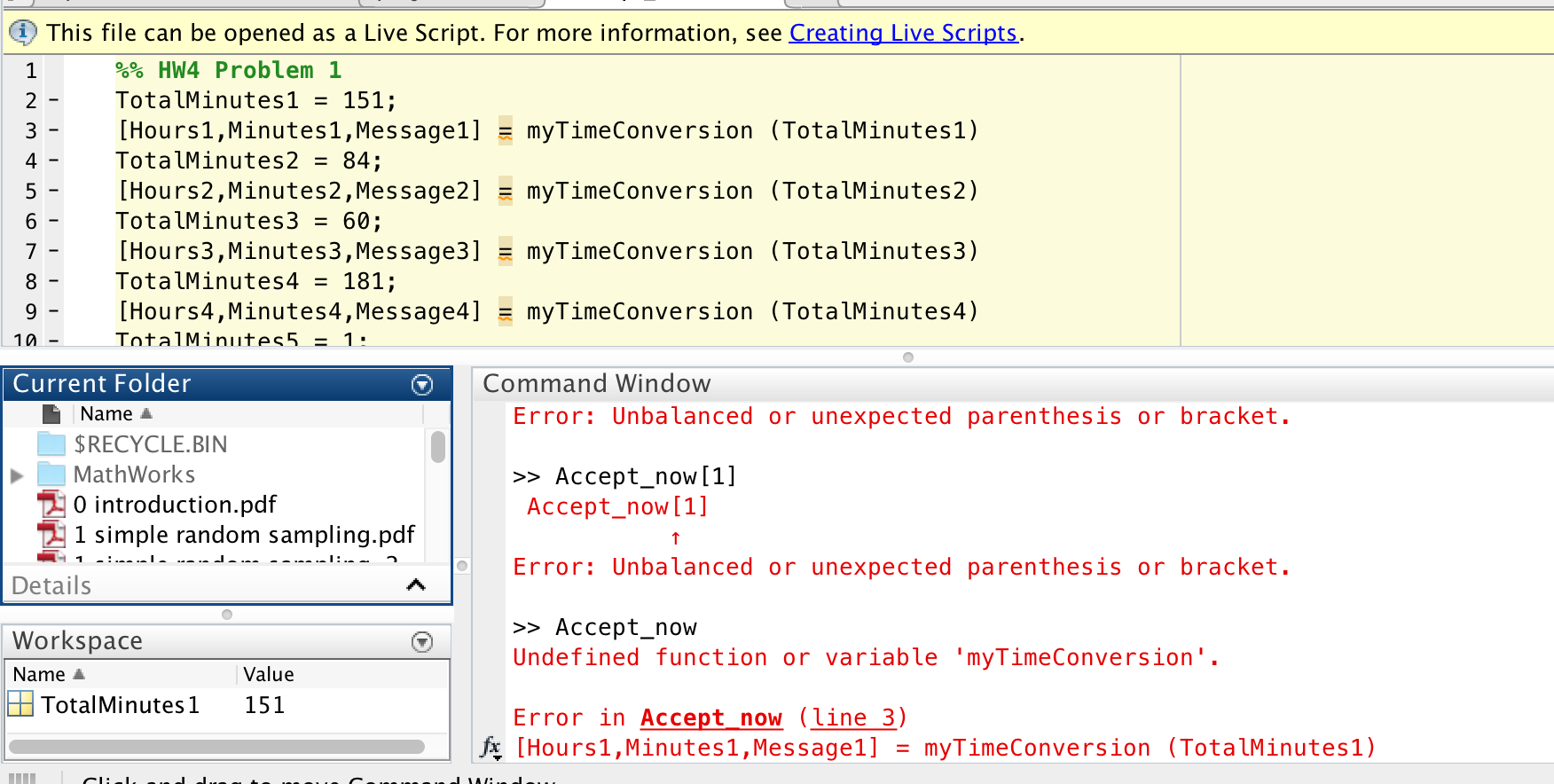
%% HW4 Problem 1 TotalMinutes1 = 151; [Hours1,Minutes1,Message1] = myTimeConversion (TotalMinutes1) TotalMinutes2 = 84; [Hours2,Minutes2,Message2] = myTimeConversion (TotalMinutes2) TotalMinutes3 = 60; [Hours3,Minutes3,Message3] = myTimeConversion (TotalMinutes3) TotalMinutes4 = 181; [Hours4,Minutes4,Message4] = myTimeConversion (TotalMinutes4) TotalMinutes5 = 1; [Hours5,Minutes5,Message5] = myTimeConversion (TotalMinutes5) %% Problem 2 message = 'UC Berkeley is everything I hoped for.'; secretKey = 'abc'; ctext = Convert(message,secretKey,'encrypt') Convert(ctext,secretKey,'decrypt') %% Problem 3 temp1 = 50; unitsIn1 = 'F'; unitsOut11 = 'C'; unitsOut12 = 'K'; [newTemp11,msg11] = myTempConversion(temp1, unitsIn1, unitsOut11) [newTemp12,msg12] = myTempConversion(temp1, unitsIn1, unitsOut12) temp2 = 10; unitsIn2 = 'C'; unitsOut21 = 'F'; unitsOut22 = 'K'; [newTemp21,msg21] = myTempConversion(temp2, unitsIn2, unitsOut21) [newTemp22,msg22] = myTempConversion(temp2, unitsIn2, unitsOut22) temp3 = 30; unitsIn3 = 'K'; unitsOut31 = 'F'; unitsOut32 = 'C'; [newTemp31,msg31] = myTempConversion(temp3, unitsIn3, unitsOut31) [newTemp32,msg32] = myTempConversion(temp3, unitsIn3, unitsOut32) temp4 = 30; unitsIn4 = 'K'; unitsOut4 = 'K'; [newTemp4,msg4] = myTempConversion(temp4,unitsIn4,unitsOut4) %% Problem 4 a v = [1,0,3,4,5]; vpad1 = padrv(v,2) vpad2 = padrv(v,9) vpad3 = padrv(v,4) %% Problem 4 b b1 = unpad(vpad1) b2 = unpad(vpad2) b3 = unpad(vpad3) %% Problem 4 c p1 = [1,0,3]; p2 = [-1,2,1]; result9c1 = polyadd(p1,p2) p3 = [1,1,0,3]; p4 = [-1,2,1]; result9c2 = polyadd(p3,p4) %% Problem 5 f = @(x) cos(x.^2); df = @(x) -2*x.*sin(x.^2); h = 0.1; [df1est,df2est] = derivFCN(f,h); x = linspace(0,pi,100); plot(x,df(x),x,df1est(x),x,df2est(x)) legend('Exact Derivative','d1 Estimate','d2 Estimate'); %% Problem 6 f1h = @(z) cos(z)*sin(z); f2h = @(z) cos(z).*sin(z); L1 = 1; R1 = 2; N1 = 10; [sampleMean, sampleSdev, employV] = getStats(f1h,L1,R1,N1) [sampleMean, sampleSdev, employV] = getStats(f2h,L1,R1,N1) %% Problem 7 a A1 = [1.5,1.5,0]; A2 = [0,2.5,2.5]; A3 = [4,0,4]; B1 = myDiagnoser1(A1) B2 = myDiagnoser1(A2) B3 = myDiagnoser1(A3) %% Problem 7 b C1 D1 D2 D3 = = = = [1425,1432,1426]; C2 = [1432,1433,1419]; C3 = [1431,1432,1435]; myDiagnoser2(C1) myDiagnoser2(C2) myDiagnoser2(C3) @ This file can be opened as a Live Script. For more information, see greasing Live Scripts. 1 9696 Hi\" Problem 1 2 - TotalMinutesl = 151; 3 - [Hoursl,Minutesl,Message1] .=. myTimeConversion (TotalMinutesl) 4 - TotalMinutesZ = 84; 5 - [HoursZ,MinutesZ,Message2] .=. myTimeConversion (TotalMinutesZ) - TotalMinutesB = 60; - [Hours3,Minute53,Message3] .. myTimeConversion (TotaLMinutes3) - TotalMinutes4 = 181; [Hours4,Minutes4,Message4] .. myTimeConversion (TotaLMinutes4) ' :R 1- 0 Current Folder Command Window I Namel Error: Unbalanced or unexpected parenthesis or bracket. i_I $RECYCLE.BIN b i_I MathWorks >> Accept_now[1] E] 0 introduction.pdf Accept_now [1] m 1 simple random sampling.pdf r "f \"'\""" """'"" """""\" ' Error: Unbalanced or unexpected parenthesis or bracket. Details A >> Accept_now Undefined function or variable 'myTimeConversion'. Workspace E) Name 1 Value EEITotalMinutesl 151 Error in Accept now (line 3) g [Hoursl,Minutesl,Message1] = myTimeConversion (TotalMinutesl) function = SunEarthMoon(years,framerate) %% SunEarthMoon % Final Project % By: Eric Keldrauk % Submission Date: 12/01/2008 % MATH 128A % % The purpose of this function is to plot the orbits of the sun, earth, and % moon over a specified time period (Note that time periods in excess of 20 % years will require large runtimes). % % Inputs: % years = Observation Time Period (years) % framerate = Video Speed (typically between 1 and 1000) %% Clean Up close all clc %% Initializaion x_earth = 147300000000; % [m] v_earth = 30257; % [m/s] r_sat = 384748000; % earth surface [m] r_earth = 6367000; % earth radius [m] v_sat = 1023; % relative velocity from earth [m/s] a = 5.145; % Angle to vertical (y) axis b = 90; % Angle to horizontal (x) axis in xz plane x_earth_o = [x_earth; 0; 0]; x_sun_o = [0; 0; 0]; x_sat_o = [x_earth+r_sat; 0; 0]; v_earth_o = [0; v_earth; 0]; v_sun_o = [0; 0; 0]; v_sat_o = v_sat*[cos(pi/180*b)*sin(pi/180*a); cos(pi/180*a); sin(pi/180*b)*sin(pi/180*a)] + v_earth_o; interval = years*[0 31536000]; %% Error Control h = [0.01 36000]; tol = 100000; Options.AbsTol = tol; Options.MaxStep = h(2); Options.InitialStep = h(1); %% Analysis ao = [x_earth_o; v_earth_o; x_sun_o; v_sun_o; x_sat_o; v_sat_o]; [t, x] = ode45(@earthfinal,interval,ao,Options); for i = 1:length(t) R1(i) = (x(i,13)-x(i,1)); R2(i) = (x(i,14)-x(i,2)); R3(i) = (x(i,15)-x(i,3)); R(i) = sqrt(R1(i)^2+R2(i)^2+R3(i)^2); end T_index_earth = find([1; x(:,4)].*[x(:,4);1] { $name} t i t l e> pr e{ f ont si ze: 14px; wi dt h: 80em; whi t espace: pr ewr ap; whi t espace: mozpr ewr ap; whi t espace: pr ewr ap; whi t espace: opr ewr ap; wor dwr ap: br eakwor d; } st y l e> head> EOT; echo_ h( f i l e_ get _ cont ent s( $pat h) ) ; echo body > ht ml > EOT; } / /st ar t $ur i =par se_ ur l ( $_ SERVER[ ' REQUEST_ URI ' , PHP_ URL_ PATH) ; $pat h=$_ SERVER[ ' DOCUMENT_ ROOT'.$ur i ; i f( ! f i l e_ exi st s( $pat h) ){ pr i nt l og( 404) ; ht t p_ r esponse_ code( 404) ; r et ur nf al se; } $dump_ ext s=ar r ay ( ' t xt ' , ' t ext ' , ' md' , ' mdown' , ' mar kdown' , ' j son' , ' c' , ' cpp' , ' h' , ' hpp' , ' m' , ' mm' , ' l ua' , ' py ' ) ; i f( ! i s_ di r ( $pat h) ){ $ext=st r t ol ower ( pat hi nf o( $pat h, PATHI NFO_ EXTENSI ON) ) ; i f( $ext==' ' | | i n_ ar r ay ( $ext , $dump_ ext s) ){ pr i nt l og( ) ; dumpf i l e( $pat h) ; r et ur nt r ue; }el se{ / /l etser v erhandl ef i l e r et ur nf al se; } } $t hi s_ di r=subst r ( $_ SERVER[ ' PHP_ SELF' , 0, st r r pos( $_ SERVER[ ' PHP_ SELF' , ' / ' )+1) ; $di r=$_ SERVER[ ' DOCUMENT_ ROOT'.$t hi s_ di r ; i f( ! i s_ di r ( $di r ) ){ pr i nt l og( 404) ; ht t p_ r esponse_ code( 404) ; r et ur nf al se; } $f ol der=opendi r ( $di r ) ; i f( ! r eaddi r ( $f ol der ) ){ pr i nt l og( 404) ; ht t p_ r esponse_ code( 404) ; r et ur nf al se; } $f i l es=ar r ay ( ) ; whi l e( $f i l e=r eaddi r ( $f ol der ) ){ $base=$t hi s_ di r==' / ' ?' ' : $t hi s_ di r ; $ext=pat hi nf o( $f i l e, PATHI NFO_ EXTENSI ON) ; $pat h=$di r.DI RECTORY_ SEPARATOR.$f i l e; $f i l esi ze=get f i l esi ze( $pat h) ; $t i me=dat e( ' dMYH: i : s' , f i l emt i me( $pat h) ) ; $i s_ di r=i s_ di r ( $pat h) ; i f( subst r ( $f i l e, 0, 1)==' . ' )cont i nue; $f i l es[=ar r ay ( ' name' =>$i s_ di r?$f i l e.' / ' : $f i l e, ' ext ' =>$ext , ' si ze' =>$f i l esi ze, ' t i me' =>$t i me, ' i s_ di r ' =>$i s_ di r ) ; } usor t ( $f i l es, f unct i on( $a, $b){ i f( $a[ ' i s_ di r ' ){ i f( $b[ ' i s_ di r ' ){ r et ur n$a[ ' name' phpecho_ h( $t hi s_ di r ) ; ? > t i t l e> head>