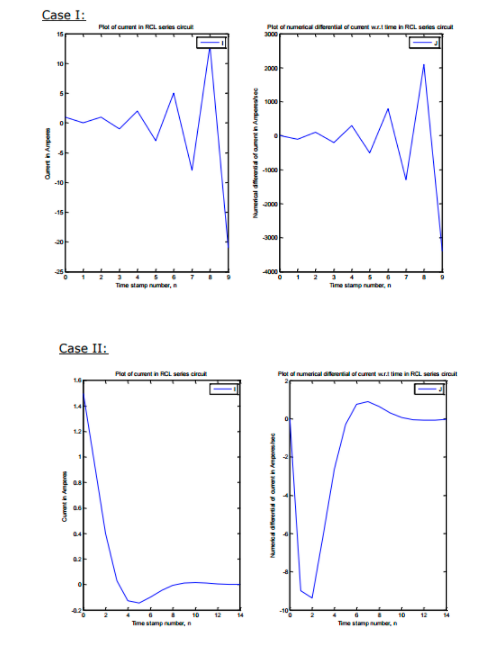
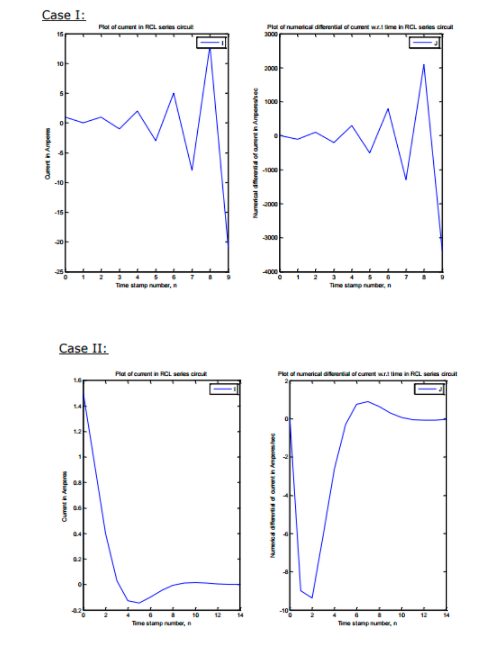
@ Hi expert i need your effort here please

\fProblem 4 (20 points) - Least-Squares Fitting with Higher-Order Polynomials In the linear least-squares regression, we are aiming at minimizing the error of the fit defined as the sum of the squares of all the residuals ry's: E(a, , d, , a ,do) = > =[[x- f(x,)]' =[[x-(atax tax tax) 1-1 where a is the number of data points, x and y are associated with / data point, and do, al, az, and, as are the four unknown coefficients to be determined. Derive the four equations that could be used to solve for the four unknown coefficients ao, al, az, and, a3. Note that you need to provide step-by-step & detailed derivations. NO partial credit will be given if you simply write down the four equations.Question 1 [3 Marks]: Given the initial-value problem 2 - 2ry y= 0(0) = 1. with exact solution 21 + 1 12 + 1 a. Use Euler's method with h = 0.1 to approximate the solution of y (use MATLAB). b. Calculate the error bound and compare the actual error at each step to the error bound. c. Use the answers generated in part (a) and linear interpolation to approximate the following values of y, and compare them to the actual value of y (0.04). d. Compute the value of h necessary for | y(t,) - wil $0.1. Question 2 [1 Mark]: Use the Modified Euler method to approximate the solutions to the above IVP with h=0.1, and compare the results to the actual values. (use MATLAB). Question 3[1 Marks]: Use the Runge-Kutta method of order four to approximate the solutions to the above IVP with h=0.1, and compare the results to the actual values (you need to find the absolute actual error only for comparison). (use MATLAB).\f