Hi I am looking for assistance with question E below.

I have provided my answer for a - d , i'm pretty sure they are correct, but i'm not sure how to do e? Can you help

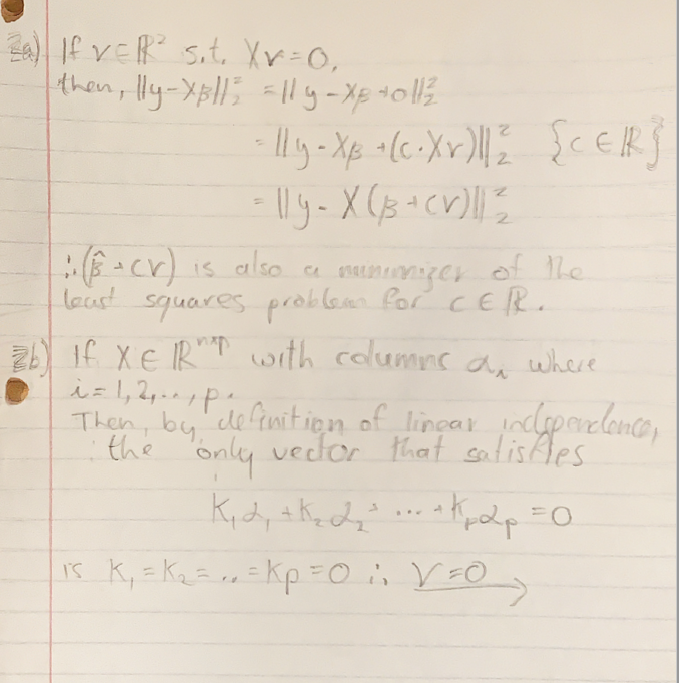
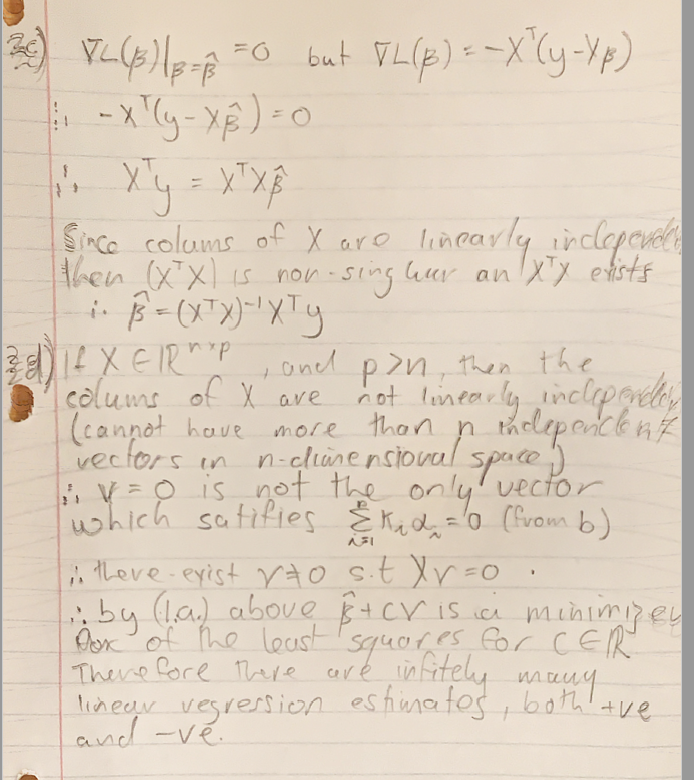
a) If VER sit. XV = O. then, 1/4-XB//? = 1ly- X8 +allz - lly - X1 + (c. Xv)//2 ECEIRS = 11 4 - X ( B + CV)//2 " ( 3 + cv ) is also a minimizer of the least squares problem for CER. 2 b) If XE RR with columns a, where i = 1 , 2 , . . , p . Then, by definition of linear inclependance, the only vector that satisfies Kid, + kids... Ahpop = 0 Is K, = K2 = .. = KP = 0 :, V= 0VL (3 ) ( B = =0 but VL(B) = - X (y-XF) : - x ( y- XB ) = 0 1, Xy = XT XB Since colums of X are linearly inclopened then ( X X) is now-sing har an X y exists 1. 13 = ( X T X )-'xTy If xER, and pon, then the colums of X are not linearly inclepenley ( cannot have more than n independent vectors in n- dimensional space ! ) ", V= O is not the only vector which satifies E kid = 0 ( from b) ". there exist to s. t XV= 0. : by (1. a. ) above B+cy is a minimizey Fox of the least squares for CER Therefore There are infitely many linear regression estimates, both +ve and - ve.2. (5 pt) Consider the following least squares problem: = arg min lly - XBl|2 (1) BERP (a) Show that if v E RP is a vector such that Xv = 0, then 3 + c.v is also a minimizer of the least squares problem, for any ce . (b) If the columns of X are linearly independent, then what vectors v E RP satisfy Xv = 0? (c) If the columns of X are linearly independent, then what vector B is the minimizer of the least squares problem? (d) Suppose that p > n. Show that there are infinitely many linear regression estimates, and that depending on which estimate we select, some coefficients can have positive or negative signs. (e) Suppose that p > n and that rank(X) = n. Show that there are infinitely many linear regression estimates, and for all of them, y = X B. Hint: See chapter 5.1 and 5.2 of https : //web. stanford. edu/~boyd/vmls/vmls . pdf