Hi, I'd like some help on my two proof attempts of the FTC for an introductory real analysis course.

Am I missing anything (assumptions, defining variables, etc) in either of these two versions? Are any of my arguments wrong? I'm unsure about differentiability in particular.

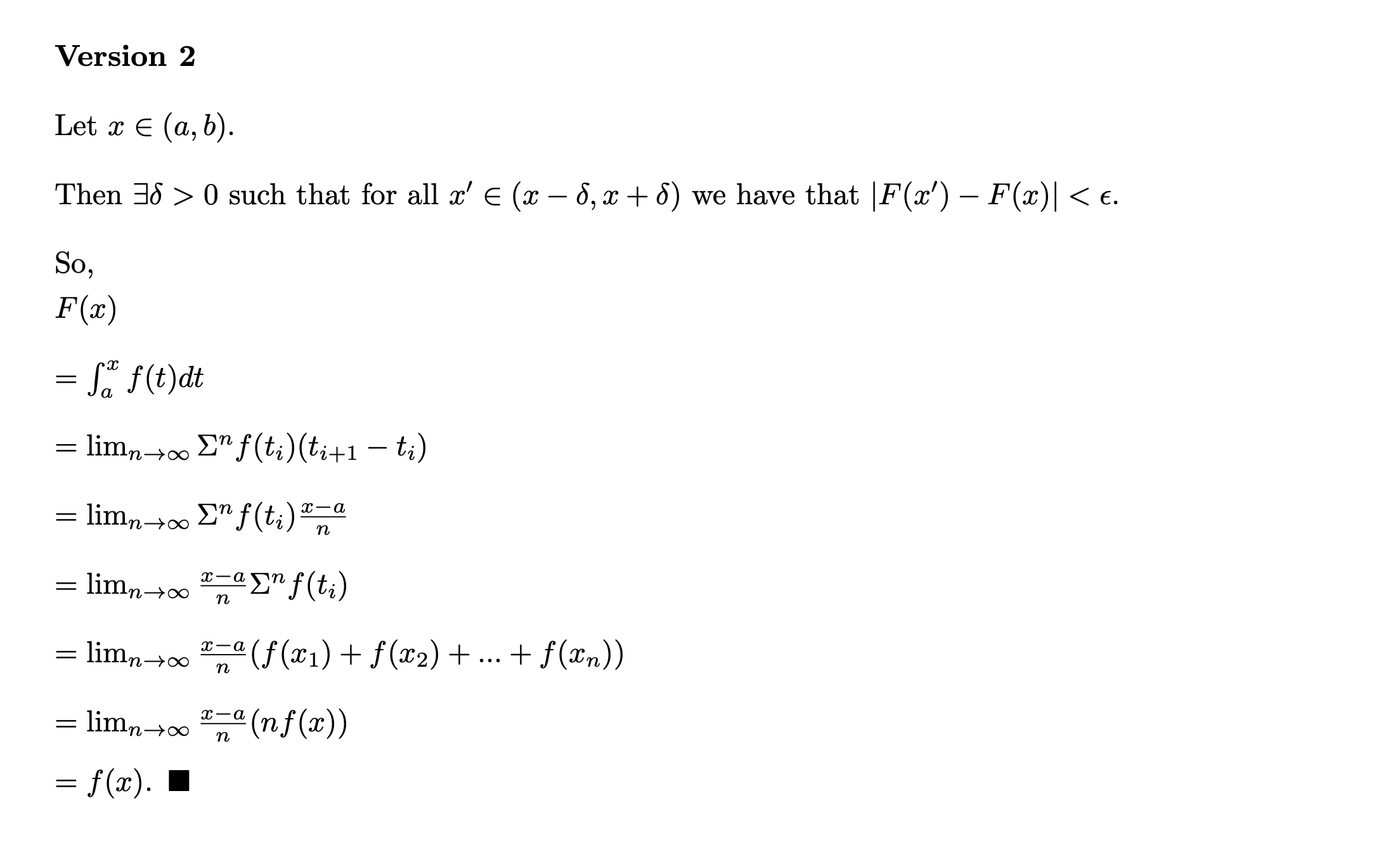
Prove that if f is a continuous function on [a, b] and F(x) = Sa f(t) dt, then for x E (a, b), F'(x) = f(x). Version 1 Let x E (a, b). Because F is continuous on [a, b], F is differentiable at x. Let h E R be given. Then, limp_ F(ath)-F(2) - F'(x). h By the definition of F, we have that: F(ath) - F(x) = Sath f(t) dt - Sa f(t) dt = fath f(t) dt. So, F' (x) = limp-0 F(ath) -F(2) h path f ( t) dt = limp =0 Jx h = limn-+0 Jx path f ( t) at h = limn-+0 Jx path f ( t) at h = limn +0 Jx rath f ( t ) at = f(2).Version 2 Let x E (a, b). Then 18 > 0 such that for all x' E (x - 8, x + 8) we have that |F(') - F(x) | con x-a En f (ti) = limn +con x - a (f ( 21 ) + f (2 2 ) + ... + f (an) ) = limn-co x -a (nf (x) ) = f(a)