Hi. I'm working with Binary arithmatic and I'm having difficulty to understand this question. I understand until multiply part. But how does the answer of multiply "111101 011110 0" becomes "000010 100010" ..? I dont really understand why. Could somebody explain to me if possible? In dividion A stands

I will report the answer if you just write the answer

I'm following this step

Question

Answer

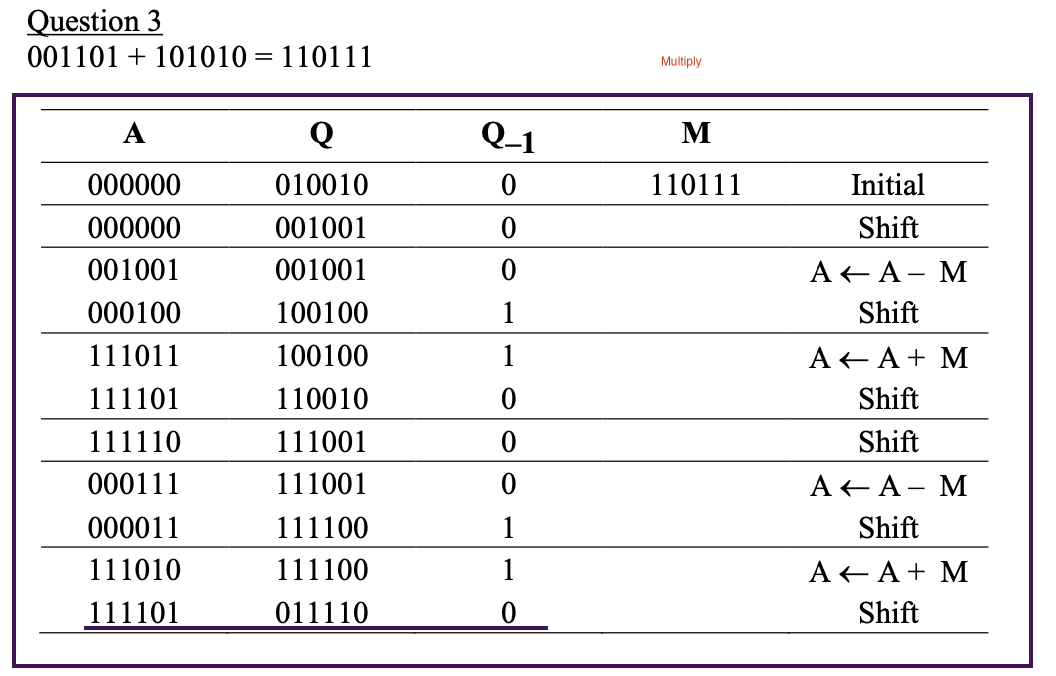
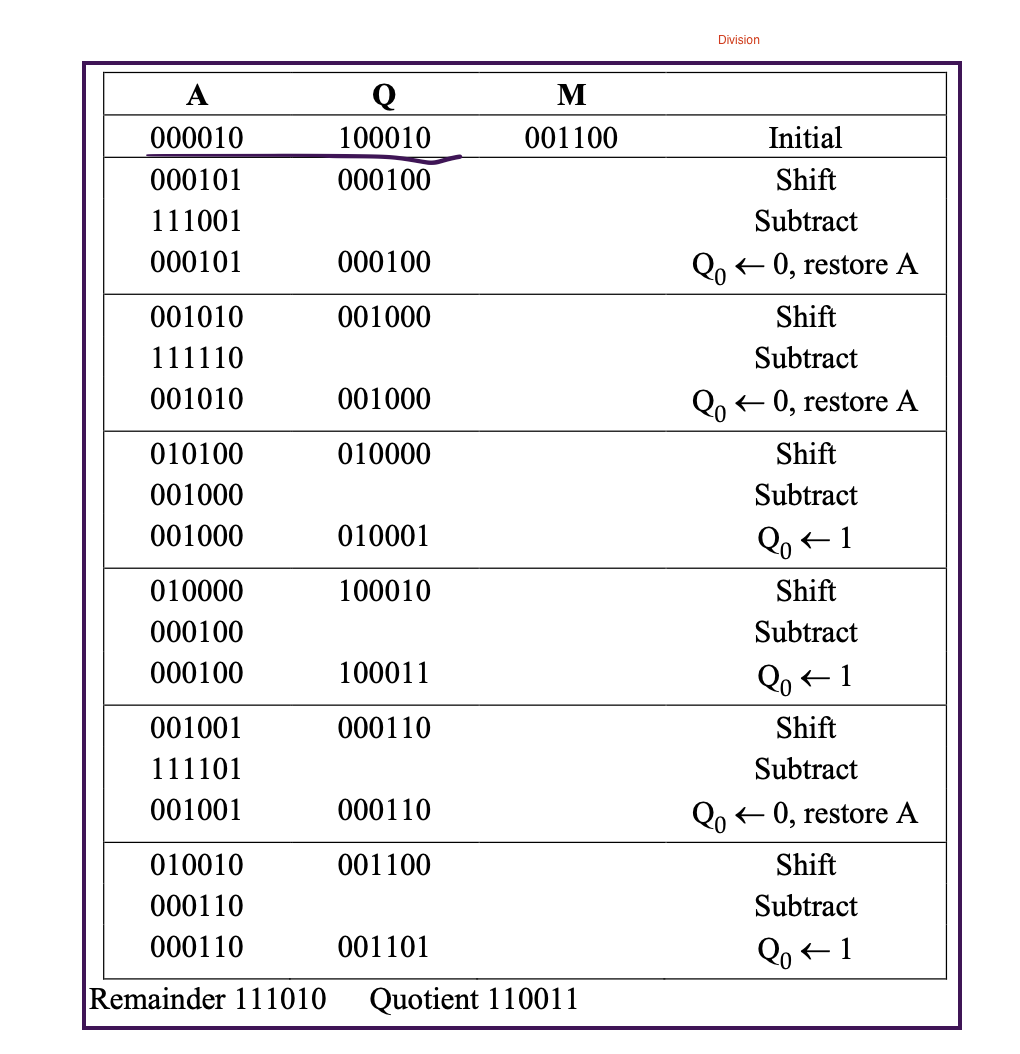
1. convert divisor and dividend into unsigned values 2. load the divisor into M register and the dividend into the A, Q registers 3. shift A, Q left 1 bit position ASL 4. perform A+ A-M 5. if A is non-negative, set Qo1 if A is negative, set Q. + 0, restore A (Last bit) 6. repeat steps 3 through 5 as many times as there are bit positions in Q (loop, depends on bit of Q) 7. remainder is in A, quotient is in 8. sign of remainder = sign of dividend (Look at the first member of dividend) 9. sign of quotient = sign of dividend x sign of divisor (Look at the first number of dividend and division Question 3 The memory with symbolic addresses and decimal integers is shown below. Address A . D 13 22 18 12 Show all the steps in performing the integer arithmetic: X= ((A - B) * C) - D Each number is represented in twos complement using 6 bits. Show the quotient and remainder in twos complement. Question 3 001101 + 101010 = 110111 Multiply A Q-1 M 110111 0 0 1 000000 000000 001001 000100 111011 111101 111110 000111 000011 111010 111101 Q 010010 001001 001001 100100 100100 110010 111001 111001 111100 111100 011110 1 0 Initial Shift A+ A- M Shift A+ A+ M Shift Shift A+ A- M Shift A+ A + M Shift 0 1 1 0 Division M 001100 A 000010 000101 111001 000101 100010 000100 000100 001000 001010 111110 001010 001000 010000 010100 001000 001000 010001 Initial Shift Subtract lot 0, restore A Shift Subtract lo + 0, restore A Shift Subtract lot 1 Shift Subtract lor 1 Shift Subtract Q00, restore A Shift Subtract lor 1 100010 010000 000100 000100 100011 000110 001001 111101 001001 000110 001100 010010 000110 000110 001101 Remainder 111010 Quotient 110011