Hi! Please do problems Q1, 3, and 4.

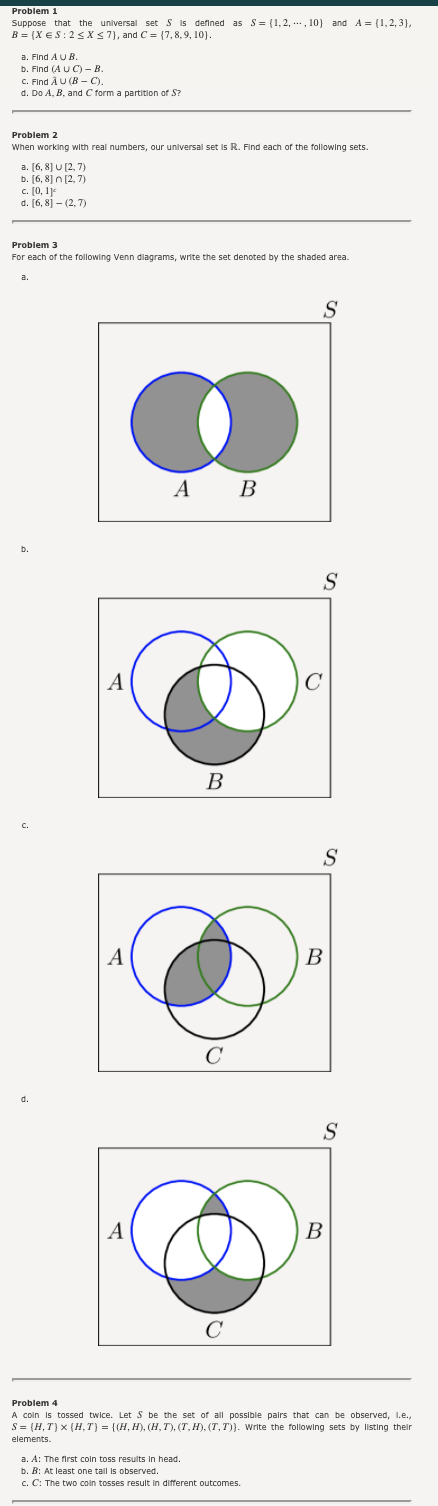
Problem 1 Suppose that the universal set $ is defined as S = (1, 2, ..., 10] and A = (1, 2,3], B = (X ES : 2 5 X S 7), and C = {7, 8,9, 10]. a. Find A UB. b. Find (A U C) - B. C. Find A U (B - C). d. Do A, B, and C form a partition of S? Problem 2 When working with real numbers, our universal set is R. Find each of the following sets. a. [6, 8] U [2, 7) b. [6, 8] n [2, 7) C. [0, 1] d. [6, 8] - (2, 7) Problem 3 For each of the following Venn diagrams, write the set denoted by the shaded area. S A B S A B A B S A B Problem 4 A coin is tossed twice. Let $ be the set of all possible pairs that can be observed, l.e., S = (H, T) x (H, T) = [(H, H), (H, T), (T, H), (T, T)). Write the following sets by listing their elements. a. A: The first coin toss results In head. b. B: At least one tall is observed. C. C: The two coin tosses result In different outcomes