Hi there looking for help to understand these questions please put the steps short

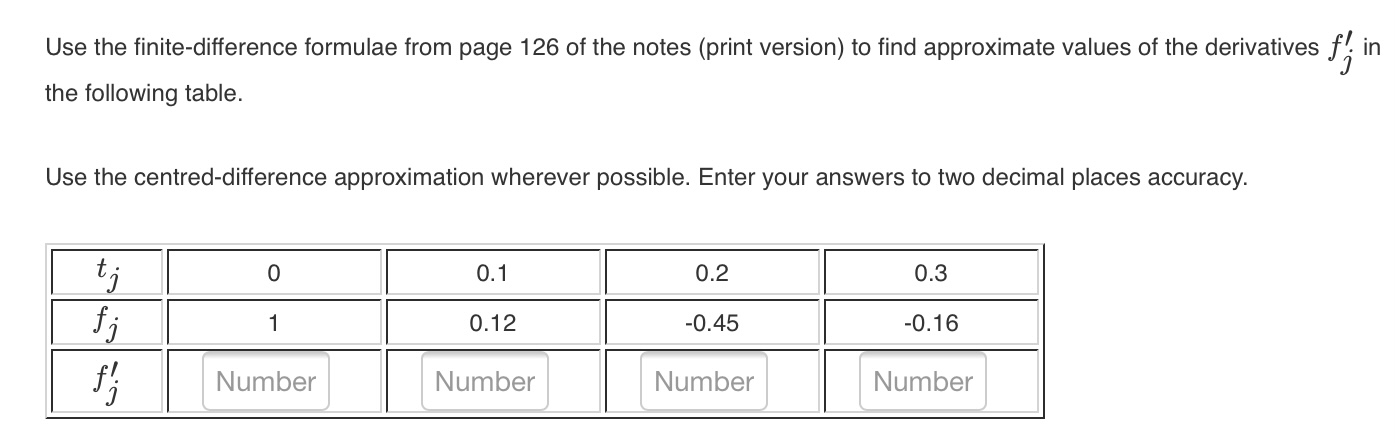
Use the finite-difference formulae from page 126 of the notes (print version) to find approximate values of the derivatives f; in the following table. Use the centred-difference approximation wherever possible. Enter your answers to two decimal places accuracy. I f;- Number Number I Number Number Let fi = f(a;), f = f'(x;), f! = f"(x;) and so on, where a; are equispaced grid points with spacing h = * j+1-aj. Applying Taylor's theorem about the point ;, f j - 2 = fj t af* +bf" + cf!" + af(iv)(t), where a = b = C = d =Suppose you are going to estimate 9 I/ cosZmdm. 0 using the trapezoidal rule. According to the error bound, what is the minimum number of points we needed to guarantee that the absolute value of the min error is less than 10*6 ? A certain function is differentiated numerically. Suppose we known that for this class of functions, the error is 001.6) as h > 0, where h is the grid spacing. When the grid spacing is halved, the error is usually expected to decrease by a factor of 2