Question: Homework 6: Problem 12 Previous Problem Problem List Next Problem (1 point) Suppose f(x) - (x - 3)(x - 6)3 + 8. Find the absolute
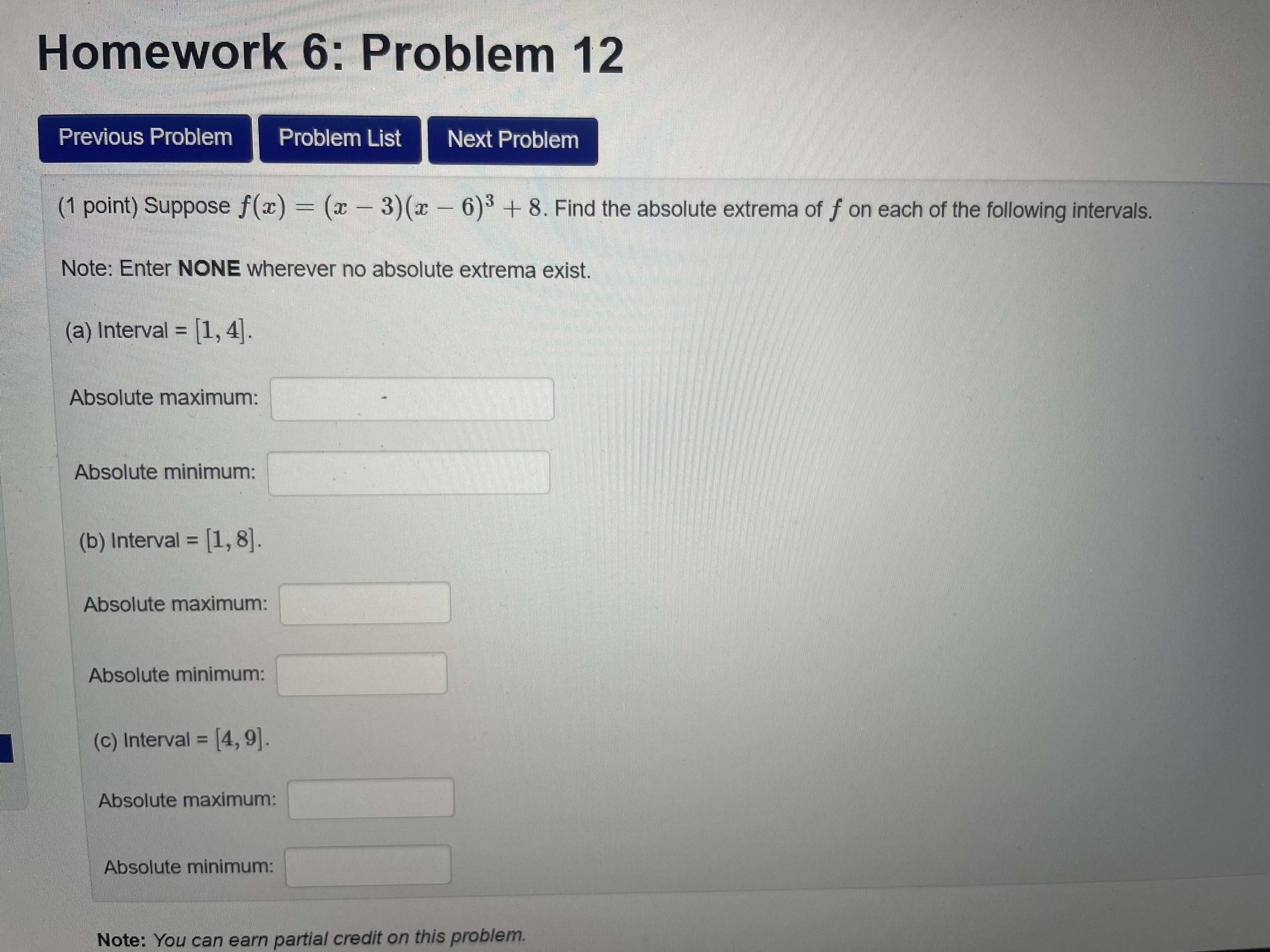
![Enter NONE wherever no absolute extrema exist. (a) Interval = [1, 4].](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679fcf4af8be_6446679fcf459c78.jpg)
![Absolute maximum: Absolute minimum: (b) Interval = [1, 8]. Absolute maximum: Absolute](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679fcf5bda99_6456679fcf536324.jpg)
![minimum: (c) Interval = [4, 9]. Absolute maximum: Absolute minimum: Note: You](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679fcf68104c_6466679fcf63e499.jpg)
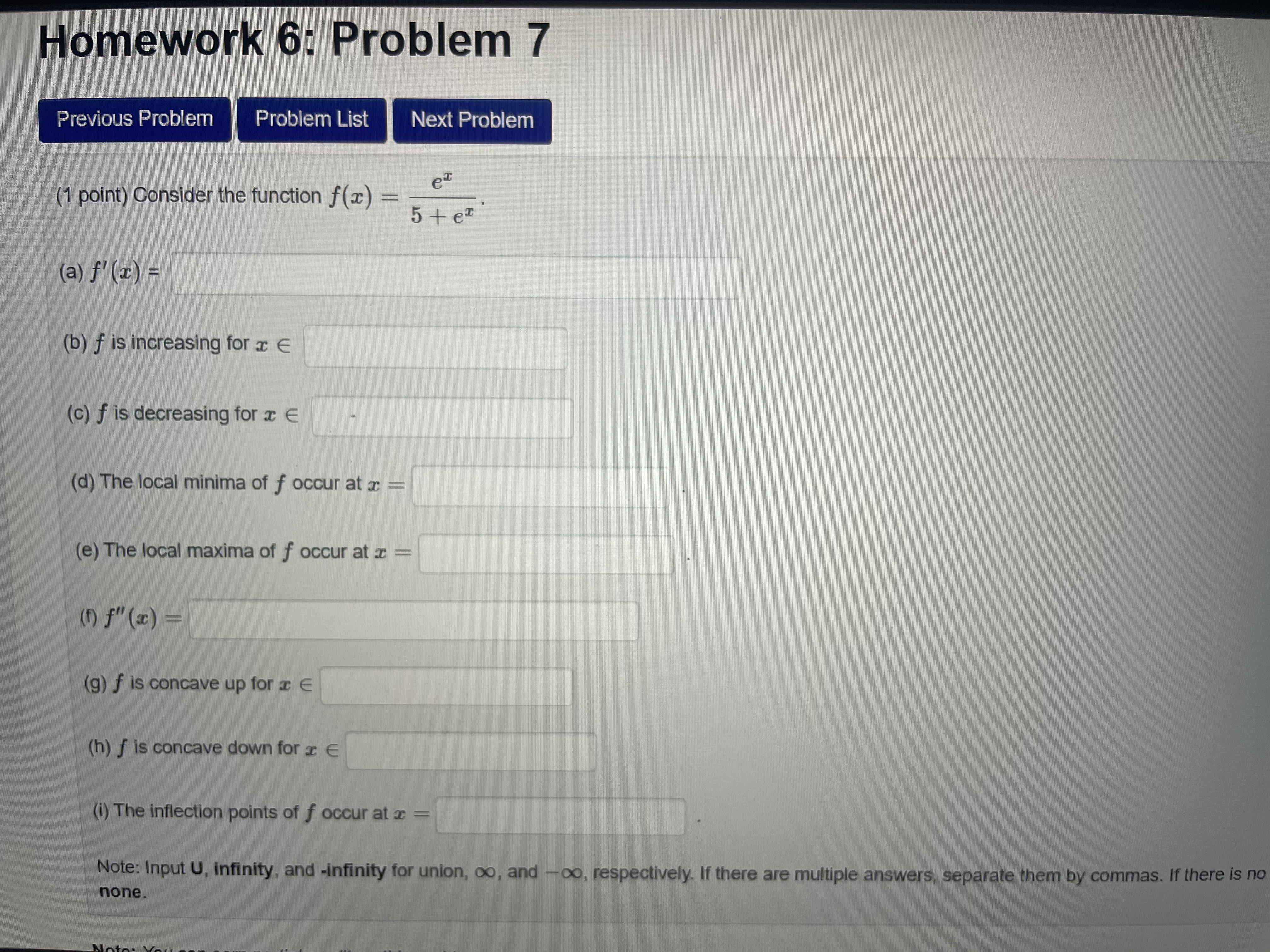
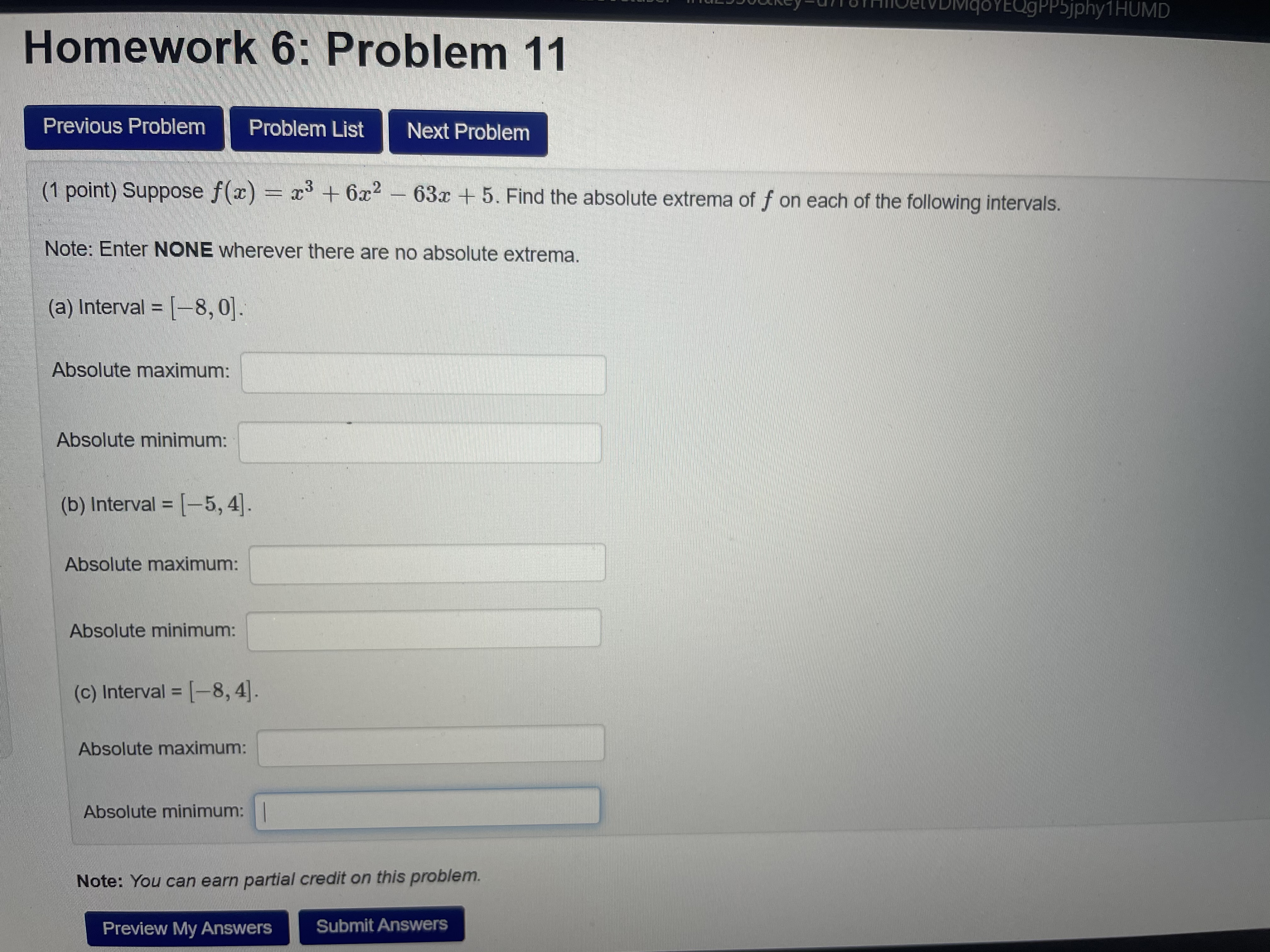
Homework 6: Problem 12 Previous Problem Problem List Next Problem (1 point) Suppose f(x) - (x - 3)(x - 6)3 + 8. Find the absolute extrema of f on each of the following intervals. Note: Enter NONE wherever no absolute extrema exist. (a) Interval = [1, 4]. Absolute maximum: Absolute minimum: (b) Interval = [1, 8]. Absolute maximum: Absolute minimum: (c) Interval = [4, 9]. Absolute maximum: Absolute minimum: Note: You can earn partial credit on this problem.Homework 6: Problem 7 Previous Problem Problem List Next Problem (1 point) Consider the function f (a) = 5+ er (a) f' (x) = (b) f is increasing for a E (c) f is decreasing for a E (d) The local minima of f occur at (e) The local maxima of f occur at x = (1) f" (x) = (g) f is concave up for a E (h) f is concave down for a E (i) The inflection points of f occur at z = Note: Input U, infinity, and -infinity for union, oo, and -co, respectively. If there are multiple answers, separate them by commas. If there is no none.DMVqoYEQgPPSjphy1HUMD Homework 6: Problem 11 Previous Problem Problem List Next Problem (1 point) Suppose f(x) - 23 + 6x2 - 63x + 5. Find the absolute extrema of f on each of the following intervals. Note: Enter NONE wherever there are no absolute extrema. (a) Interval = [-8, 0]. Absolute maximum: Absolute minimum: (b) Interval = [-5, 4]. Absolute maximum: Absolute minimum: (c) Interval = [-8, 4]. Absolute maximum: Absolute minimum: Note: You can earn partial credit on this problem. Preview My Answers Submit Answers
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


