Question: homework help (1 point) Solve the following differential equation by variation of parameters. Fully evaluate all integrals. y + 637' + 9y = 3x. a.

homework help

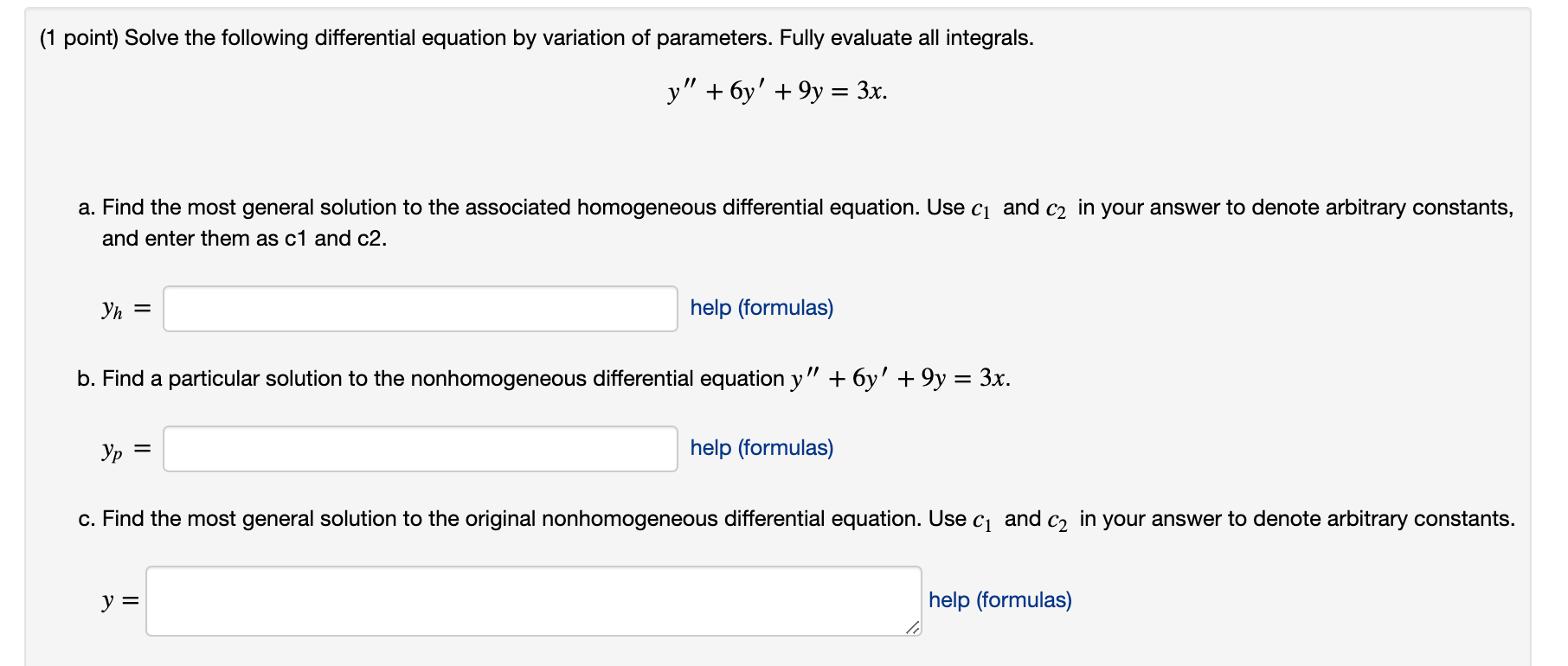
(1 point) Solve the following differential equation by variation of parameters. Fully evaluate all integrals. y" + 637' + 9y = 3x. a. Find the most general solution to the associated homogeneous differential equation. Use c1 and cz in your answer to denote arbitrary constants, and enter them as c1 and c2. 3'}: = help (formulas) b. Find a particular solution to the nonhomogeneous differential equation y\" + 6y' + 9y = 3x. yp = help (formulas) c. Find the most general solution to the original nonhomogeneous differential equation. Use cl and (:2 in your answer to denote arbitrary constants. y = help (formulas) /

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

In this task, you will research and present your findings on ammonium lauryl sulfate, also called ammonium dodecyl sulfate.Ammonium lauryl sulfate is a type of surfactant, a cleaning chemical...

homework help (1 point) Solve the following differential equation by variation of parameters. Fully evaluate all integrals. y\" + 16y = sec(4x). a. Find the most general solution to the associated...

hw6: Problem 1 Previous Problem Problem List Next Problem (1 point) Find y as a function of a if y" - 13y" + 42y' = 60er, y(0) - 20, y' (0) = 30, y" (0) = 11. Preview My Answers Submit Answers You...

Please see attachment for question. Entered Answer Preview Result Message c1*cos(2*x)+c2*sin(2*x) c1 cos(2x) + c2 sin(2x) correct (1/4)*cos(2*x)*log(cos(2*x))+(1/2)*x*sin(2*x) - cos(2x) log(cos(2x))...

Please see attachment for question. (1 point) Solve the following differential equation by variation of parameters. Fully evaluate all integrals. y" +8y' +16y=4x. a. Find the most general solution to...

point) Solve the following differential equation by variation of parameters. Fully evaluate all integrals. y" + 6y' + 9y = 31. a. Find the most general solution to the associated homogeneous...

Solve the following differential equation by variation of parameters. Fully evaluate all integrals. y" + 6y' + 9y = 3r. a. Find the most general solution to the associated homogeneous differential...

TT Variation of Parameters: Problem 1 ( 1 point ) Results for this submission 2 of the answers are NOT correct. Solve the following differential equation by variation of parameters. Fully evaluate...

HELPP HOMEWORK NOT for TUTOR: dont submit if you dont do full THEM OR BAD RATE And in full explanation show all explanation Use the method of partial derivatives to find the critical points and...

UNIVERISTY HELPP IN HERE NOT for TUTOR: dont submit if you dont do full THEM OR BAD RATE And in full explanation show all your work Solve the following system of nonlinear equations:x^2 + y^2 = 9 x^2...

HOMEWORK NOT for TUTOR: dont submit if you dont do full THEM OR BAD RATE And in full explanation show all your work Solve the following system of nonlinear equations:x^2 + y^2 = 9 x^2 - y^2 = 1 Find...

Determine the taxable income of each of the following dependents for 2011: a. Louis is 12 and receives $1,150 in interest income. b. Jackson is 16. He earns $2,000 from his newspaper route and...

Classify each of the following costs as a direct cost or an indirect cost assuming the cost object is the Garden Department of a local hardware store. a. Garden managers salary b. Cost of shopping...

When a CPA owns stock of a client, this may create a _ _ _ _ _ _ .

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...