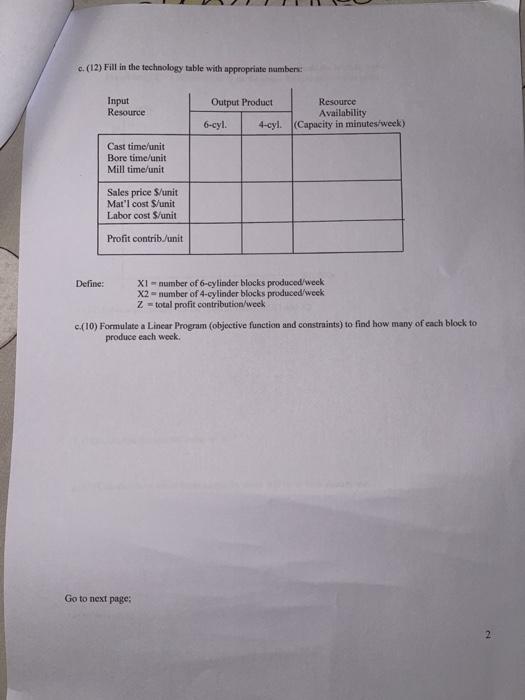
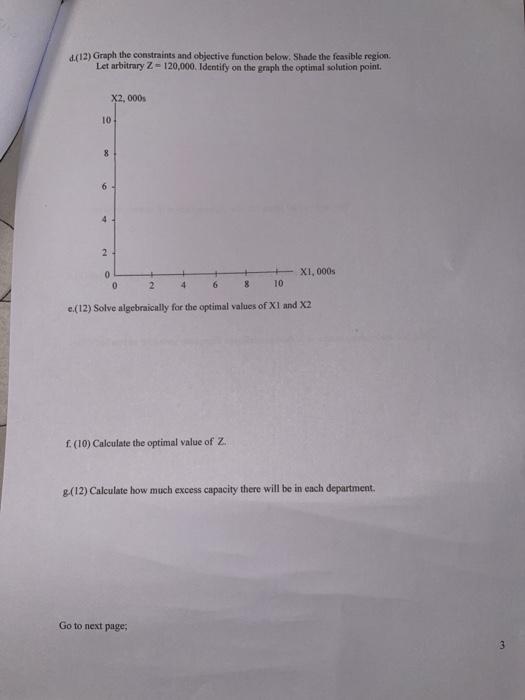
Homework - Linear Programming Application The Auto Engine Block (AEB) Company manufactures aluminum six cylinder and four cylinder engine blocks for the major automobile companies in the Detroit area. The production of an engine block consists of three sequential steps: 1. Cast the block 2. Bore the cylinders 3. Mill the mounting surfaces. The company currently employs 135 workers with 20 assigned to the Casting department, 75 assigned to the Boring department and 40 assigned to the Milling department. All departments operate for eight hours/day, five days/week. Each six cylinder block requires 8 minutes of labor time to cast, 18 minutes to bore and 24 minutes to mill. The four cylinder block takes 12 minutes of labor to cast, 18 minutes to bore and 12 minutes to mill. Six cylinder blocks sell for $75.00 each and use $20.00 of material. Four cylinder blocks sell for $56.00 each and use $13.40 of material. The company pays all workers $18 per hour. Assume that AEB can sell as many of either block as it can produce. a.(6) Calculate the labor capacity in minutes per week in each department: Cast: Bore: Mill: b.(6) Calculate the labor cost per minute Go to next page: c. (12) Fill in the technology table with approprinte numbers Input Resource Output Product Resource Availability (Capacity in minutes/week) 6-cyl. 4-cyl. Cast time/unit Bore time/unit Mill time/unit Sales price S/unit Mat'l cost S/unit Labor cost S/unit Profit contrib/unit Define: XI - number of 6-cylinder blocks produced/week X2 - number of 4-cylinder blocks produced/week Z = total profit contribution/week c.(10) Formulate a Linear Program (objective function and constraints) to find how many of each block to produce each week. Go to next page: (12) Graph the constraints and objective function below. Shunde the feasible region. Let arbitrary Z - 120,000. Identify on the graph the optimal solution point X2,000 10 8 6 2 X1,000s 0 0 2 6 8 10 c.(12) Solve algebraically for the optimal values of X1 and X2 1. (10) Calculate the optimal value of Z 8.(12) Calculate how much excess capacity there will be in each department. Go to next page: 3 (12) At what percent of capacity will each department operate? At what percent of overall capacity will the entire factory operate? h.(4) Identify which department(s) are the bottleneck operations 1.(4) What will be the actual total profit contribution/week if no excess workers are laid off? Homework - Linear Programming Application The Auto Engine Block (AEB) Company manufactures aluminum six cylinder and four cylinder engine blocks for the major automobile companies in the Detroit area. The production of an engine block consists of three sequential steps: 1. Cast the block 2. Bore the cylinders 3. Mill the mounting surfaces. The company currently employs 135 workers with 20 assigned to the Casting department, 75 assigned to the Boring department and 40 assigned to the Milling department. All departments operate for eight hours/day, five days/week. Each six cylinder block requires 8 minutes of labor time to cast, 18 minutes to bore and 24 minutes to mill. The four cylinder block takes 12 minutes of labor to cast, 18 minutes to bore and 12 minutes to mill. Six cylinder blocks sell for $75.00 each and use $20.00 of material. Four cylinder blocks sell for $56.00 each and use $13.40 of material. The company pays all workers $18 per hour. Assume that AEB can sell as many of either block as it can produce. a.(6) Calculate the labor capacity in minutes per week in each department: Cast: Bore: Mill: b.(6) Calculate the labor cost per minute Go to next page: c. (12) Fill in the technology table with approprinte numbers Input Resource Output Product Resource Availability (Capacity in minutes/week) 6-cyl. 4-cyl. Cast time/unit Bore time/unit Mill time/unit Sales price S/unit Mat'l cost S/unit Labor cost S/unit Profit contrib/unit Define: XI - number of 6-cylinder blocks produced/week X2 - number of 4-cylinder blocks produced/week Z = total profit contribution/week c.(10) Formulate a Linear Program (objective function and constraints) to find how many of each block to produce each week. Go to next page: (12) Graph the constraints and objective function below. Shunde the feasible region. Let arbitrary Z - 120,000. Identify on the graph the optimal solution point X2,000 10 8 6 2 X1,000s 0 0 2 6 8 10 c.(12) Solve algebraically for the optimal values of X1 and X2 1. (10) Calculate the optimal value of Z 8.(12) Calculate how much excess capacity there will be in each department. Go to next page: 3 (12) At what percent of capacity will each department operate? At what percent of overall capacity will the entire factory operate? h.(4) Identify which department(s) are the bottleneck operations 1.(4) What will be the actual total profit contribution/week if no excess workers are laid off