how can i get widget rigrh?

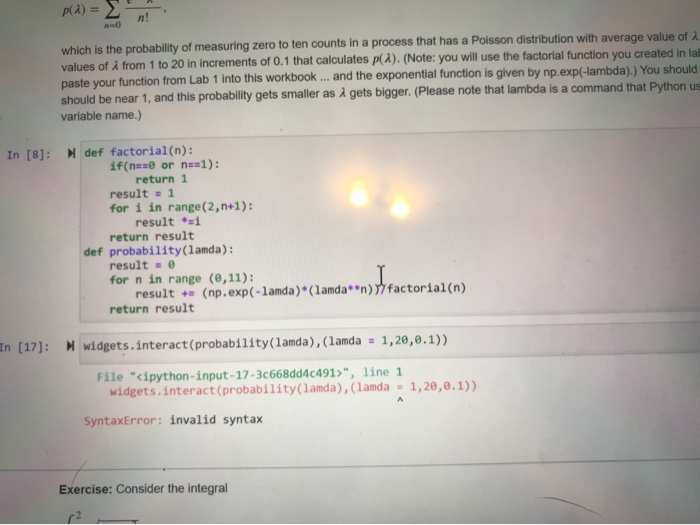
pla) = 2 n ! which is the probability of measuring zero to ten counts in a process that has a Poisson distribution with average value of values of from 1 to 20 in increments of 0.1 that calculates p). (Note: you will use the factorial function you created in paste your function from Lab 1 into this workbook ... and the exponential function is given by np.exp(-lambda).) You should should be near 1, and this probability gets smaller as i gets bigger. (Please note that lambda is a command that Python u variable name.) In [8]: Ndef factorial(n): if(n== or nael): return 1 result = 1 for i in range(2, n+1): result i return result def probability(lamda): result = for n in range (@,11): result + (np.exp(-lamda) (lamda**n) factorial(n) return result En [17]: W widgets.interact (probability(lamda),(lamda = 1,20,0.1)) File "", line 1 widgets.interact(probability (lamda), (lamda = 1,20,0.1)) SyntaxError: invalid syntax Exercise: Consider the integral (2