How can I solve the below problems?

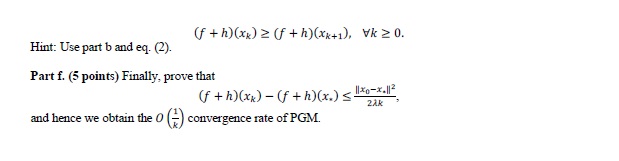
Question 2. Proximal gradient method (30 points) In this module, we have learned the proximal gradient method (PGM) and we know that it has o () convergence rate. This question is designed to guide you go through the process of proving this convergence rate rigorously. Recall the proximal operator is defined as proxy (x): = argmin f(u) +|u - x| |2:uER", VxER". Our goal is to minimizeff(u) + h(u):ue R"] (1) where h is a proper lower semicontinuous convex function and f is a smooth convex function on dom(h). We assume that f has L-Lipschitz continuous gradient, i.e., [lvf(x) - Vf(y)ll s Lllx - yll, Vx,y E dom(h), and hence for every x, y E dom(h), f ( x) st, (x;y ) + = llx-yl/2 (2) where f,(x; y) = f() + (Vf(v).x ->). Recall that PGM with a constant prox stepsize 1 ( 1/L) recursively computes its iterates according to XX+1 = proxin (Xk - AVf (xx))- Part a. (5 points) Prove that an iteration of PGM is equivalent to Xx+1 = argmin fy(u; xx) + h(u) +=, llu - xxll2: u e R". and the objective function is =-strongly convex (See the definition of strongly convex https://en.wikipedia.org/wiki/Convex_function#Strongly_convex_functions). Part b. (5 points) Prove that f, (u; x,) + h(u) +=llu - xxll? > f,(*+;xx) + h(xx+1) +=llxx+1 - xxll? +-llu -xx+ill? Hint: You can use the following result: Let f be a proper closed and u-strongly convex function for some > 0. Then f ( x) 2f (x.) +=1/x-x.1/2 for all x E dom(f), where x. is the unique minimizer of f. Part c. (5 points) Assume that A $ 1/L, then prove that (f + h ) (x.)+,, llxx - x. 12 2 (f + h ) (xx+1) + h(xx+1)+7,llxx+1 -x.1/2 where x. is a minimizer of eq. (1). Hint: You could use eq. (2). Part d. (5 points) Prove that [ f + h ) ( x ) - k(f +h)(x)s Ilxo - x.112 2.1 where xo is the initial point of PGM. Part e. (5 points) Prove that PGM has the descent property, ie.,(f + h ) (x) > (f + h)(xx+1). Vk 20. Hint: Use part b and eq. (2). Part f. (5 points) Finally, prove that ( f + h ) ( xx ) - (f + h) (x.)s 2Ak and hence we obtain the o () Convergence rate of PGM