How do i do this?

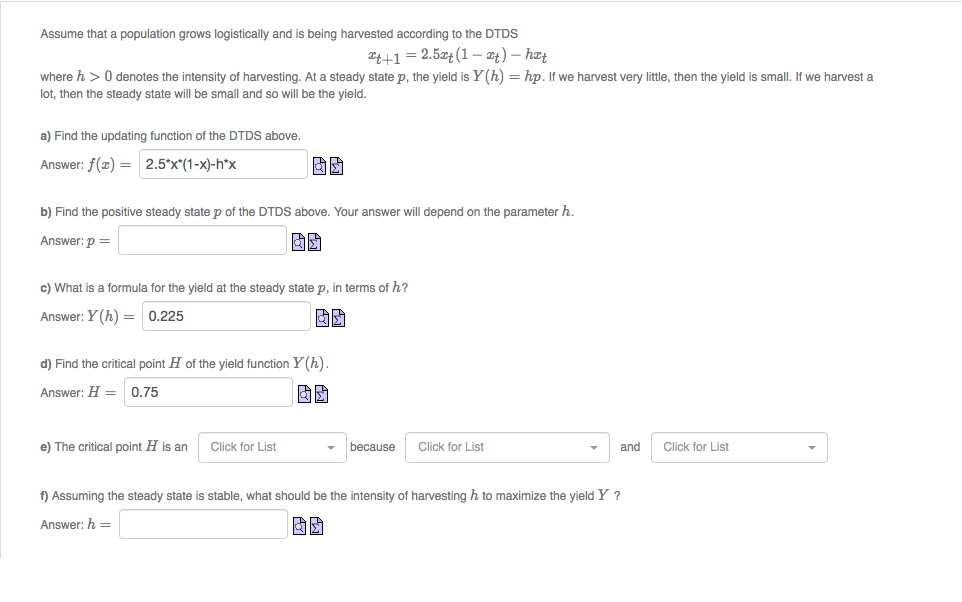
Assume that a population grows logistically and is being harvested according to the DTDS "t+1 = 2.5x4 (1 - at) - hat where h > 0 denotes the intensity of harvesting. At a steady state p, the yield is Y (h) = hp. If we harvest very little, then the yield is small. If we harvest a lot, then the steady state will be small and so will be the yield. a) Find the updating function of the DTDS above. Answer: f(x) = 2.5*x*(1-x)-h*x b) Find the positive steady state p of the DTDS above. Your answer will depend on the parameter h. Answer: P = c) What is a formula for the yield at the steady state p, in terms of h? Answer: Y (h) = 0.225 d) Find the critical point H of the yield function Y (h). Answer: H = 0.75 e) The critical point H is an Click for List because Click for List and Click for List f) Assuming the steady state is stable, what should be the intensity of harvesting h to maximize the yield Y ? Answer: h =