How do I find the cartesian equation for both the tangent and normal in this question as shown below?

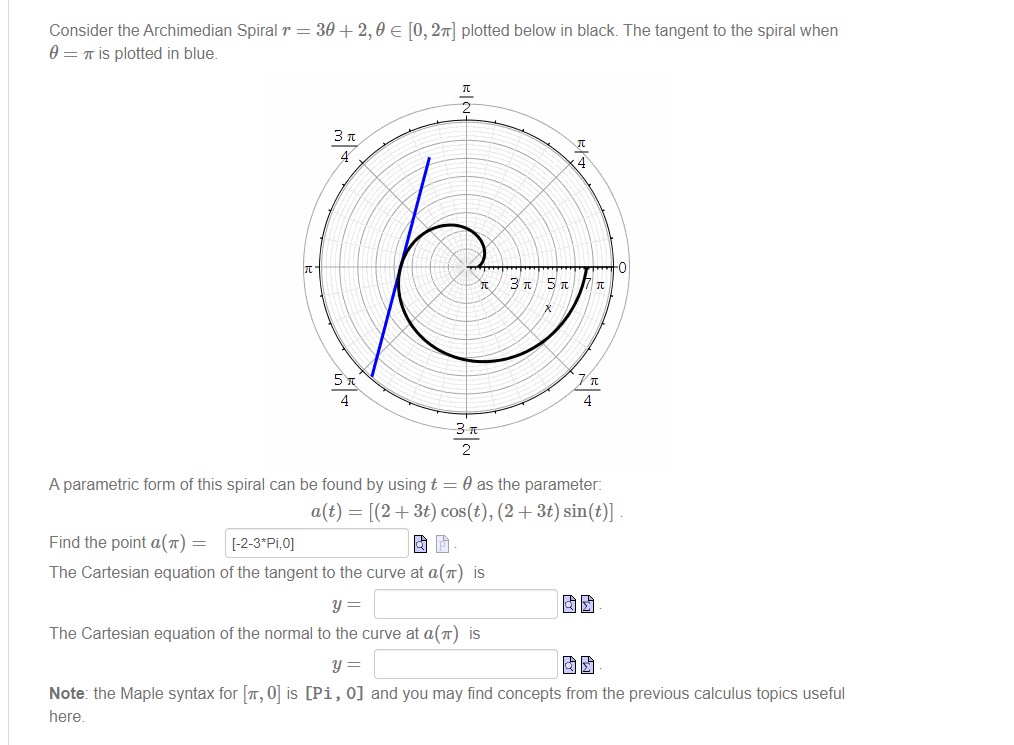
Consider the Archimedian Spiral r = 30 + 2, 0 E [0, 2x] plotted below in black. The tangent to the spiral when 0 = 7 is plotted in blue. -0 5 1 4 4 3 At A parametric form of this spiral can be found by using t = 0 as the parameter: a(t) = [(2 + 3t) cos(t), (2 + 3t) sin(t)] . Find the point a(7) = [-2-3*Pi,0] & G. The Cartesian equation of the tangent to the curve at a(7) is y = The Cartesian equation of the normal to the curve at a(7) is y = Note: the Maple syntax for [7, 0] is [Pi , 0] and you may find concepts from the previous calculus topics useful here