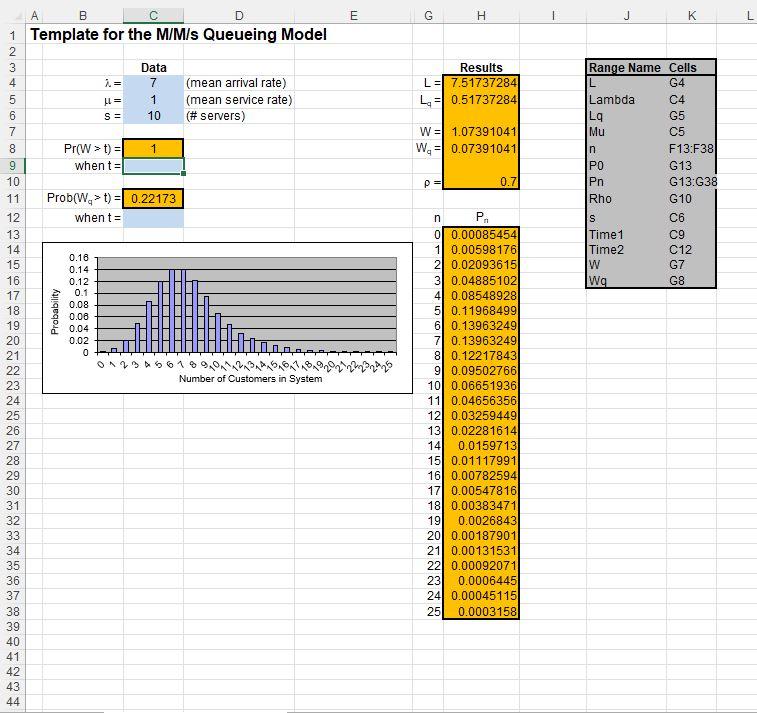
How do I solve for when t = ?

Reducing In-Process Inventory Jim Wells, vice-president for manufacturing of the Northern Airplane Company, is exasperated. His walk through the company's most important plant this morning has left him in a foul mood. However, he now can vent his temper at Jerry Carstairs, the plant's production manager, who has just been summoned to Jim's office. "Jerry, I just got back from walking through the plant, and I am very upset." "What is the problem, Jim?" "Well, you know how much I have been emphasizing the need to cut down on our in-process inventory." "Yes, we've been working hard on that," responds Jerry. "Well, not hard enough!" Jim raises his voice even higher. "Do you know what I found by the presses?" "No." "Five metal sheets still waiting to be formed into wing sections. And then, right next door at the inspection station, 13 wing sections. The inspector was inspecting one of them, but the other 12 were just sitting there. You know we have a couple hundred thousand dollars tied up in each of those wing sections. So between the presses and the inspection station, we have a few million bucks worth of terribly expensive metal just sitting there. We can't have that!" The chagrined Jerry Carstairs tries to respond. "Yes, Jim, I am well aware that that inspection station is a bottleneck. It usually isn't nearly as bad as you found it this morning, but it is a bottleneck. Much less so for the presses. You really caught us on a bad morning." "I sure hope so," retorts Jim, but you need to prevent anything nearly this bad happening even occasionally. What do you propose to do about it?" Jerry now brightens noticeably in his response. "Well actually, I've already been working on this problem. I have a couple proposals on the table and I have asked an operations research analyst on my staff to analyze these proposals and report back with recommendations." "Great," responds Jim, "glad to see you are on top of the problem. Give this your highest priority and report back to me as soon as possible." "Will do," promises Jerry Here is the problem that Jerry and his OR analyst are addressing. Each of 10 identical presses is being used to form wing sections out of large sheets of specially processed metal. The sheets arrive randomly to the group of presses at a mean rate of 7 per hour. The time required by a press to form a wing section out of a metal sheet has an exponential distribution with a mean of 1 hour. When finished, the wing sections arrive randomly at an inspection station at the same mean rate as the metal sheets arrived at the presses (7 per hour). A single inspector has the full-time job of inspecting these wing sections to make sure they meet specifications. Each inspection takes her 7 % minutes, so she can inspect 8 wing sections per hour. This inspection rate has resulted in a substantial average amount of in-process inventory at the inspection station (i.e., the average number of wing sheets waiting to complete inspection is fairly large), in addition to that already found at the group of machines. MacRook Pro wang summoned to Jim's office. Jerry, I just got back from walking through the plant, and I am very upset." "What is the problem, Jim?" "Well, you know how much I have been emphasizing the need to cut down on our in-process inventory." "Yes, we've been working hard on that," responds Jerry. "Well, not hard enough!" Jim raises his voice even higher. "Do you know what I found by the presses?" "No." "Five metal sheets still waiting to be formed into wing sections. And then, right next door at the inspection station, 13 wing sections. The inspector was inspecting one of them, but the other 12 were just sitting there. You know we have a couple hundred thousand dollars tied up in each of those wing sections. So between the presses and the inspection station, we have a few million bucks worth of terribly expensive metal just sitting there. We can't have that!" The chagrined Jerry Carstairs tries to respond. "Yes, Jim, I am well aware that that inspection station is a bottleneck. It usually isn't nearly as bad as you found it this morning, but it is a bottleneck. Much less so for the presses. You really caught us on a bad morning." "I sure hope so," retorts Jim, "but you need to prevent anything nearly this bad happening even occasionally. What do you propose to do about it?" Jerry now brightens noticeably in his response. "Well actually, I've already been working on this problem. I have a couple proposals on the table and I have asked an operations research analyst on my staff to analyze these proposals and report back with recommendations." "Great," responds Jim, glad to see you are on top of the problem. Give this your highest priority and report back to me as soon as possible." "Will do," promises Jerry. Here is the problem that Jerry and his OR analyst are addressing. Each of 10 identical presses is being used to form wing sections out of large sheets of specially processed metal. The sheets arrive randomly to the group of presses at a mean rate of 7 per hour. The time required by a press to form a wing section out of a metal sheet has an exponential distribution with a mean of 1 hour. When finished, the wing sections arrive randomly at an inspection station at the same mean rate as the metal sheets arrived at the presses (7 per hour). A single inspector has the full-time job of inspecting these wing sections to make sure they meet specifications. Each inspection takes her 7 % minutes, so she can inspect 8 wing sections per hour. This inspection rate has resulted in a substantial average amount of in-process inventory at the inspection station (i.e., the average number of wing sheets waiting to complete inspection is fairly large), in addition to that already found at the group of machines. The cost of this in-process inventory is estimated to be $8 per hour for each metal sheet at the presses or each wing section at the inspection station. Therefore, Jerry Carstairs has made three alternative proposals to reduce the average level of in-process inventory. Proposal 1 is to use slightly less power for the presses (which would increase their average time to form a wing section to 1.2 hours), so that the inspector can keep up with their output better. This also would reduce the cost of the power for running each machine from $7.00 to $6.50 per hour. The arrival rate for the inspection station would not change and it's still 7 per hour. Proposal 2 is use more power for the presses. This would increase the cost of the power for running each machine to $7.50 per hour while decreasing the average time to form a wing section to 0.8 hour. Again, this would not change the arrival rate for the inspection station. Proposal 3 is to substitute a certain inspector for this task. He is somewhat faster, so he should keep up better. His inspection time would have an exponential distribution with a mean of 7 minutes. This inspector is in a job classification that calls for a total compensation (including benefits) of $19 per hour, whereas the current inspector is in a lower job classification where the compensation is $17 per hour. You are the OR analyst on Jerry carstair's staff who has been asked to analyze this problem. He wants you to "use the latest OR techniques to see how much each proposal would cut down on in-process inventory and then make your recommendations." (a) To provide a basis of comparison, begin by evaluating the status quo. Determine the expected amount of in-process inventory at the presses and at the inspection station. Then calculate the expected total cost per hour when considering all of the following: the cost of the in- process inventory, the cost of the power for running the presses, and the cost of the inspector. (b) What would be the effect of proposal 1? Why? Make specific comparisons to the results from part (a). Explain this outcome to Jerry Carstairs. (c) Determine the effect of proposal 2. Make specific comparisons to the results from part (a). Explain this outcome to Jerry Carstairs. (d) Do the same analysis for proposal 3. (e) Make your recommendations for reducing the average level of in-process inventory at the inspection station and at the group of machines. Be specific in your recommendations, and support them with quantitative analysis you have done in parts (a) to (d). B D E G H K 1 Template for the M/M/s Queueing Model i = Data 7 1 10 Results L = 7.51737284 L = 0.51737284 NO 000 UN (mean arrival rate) (mean service rate) (# servers) = S = 2 3 4 5 6 7 8 9 10 11 W = 1.07391041 W = 0.07391041 Range Name Cells L G4 Lambda C4 La G5 Mu C5 n F13:F38 PO G13 Pn G13:G38 Rho G10 1 Pr(w>t) = when t = 0.7 Prob(W,>t) = 0.22173 when t= n Time 1 Time2 W 12 13 14 15 16 17 18 19 20 21 C6 C9 C12 G7 G8 00 OULAW Probability 0.16 0.14 0.12 0.1 0.08 0.00 0.04 0.02 0 Fi ALLE 22 Number of Customers in System 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 P. 0 0.00085454 1 0.00598176 21 0.020936151 31 0.04885102 41 0.08548928 5 0.11968499 61 0.13963249 7 0.13963249 8 0.12217843 9 0.09502766 10 0.06651936 11 0.04656356 121 0.03259449 131 0.02281614 14 0.0159713 15 0.01117991 16 0.00782594 171 0.00547816 18 0.00383471 19 0.0026843 201 0.00187901 21 0.00131531 22 0.00092071 23 0.0006445 24 0.00045115 25 0.0003158 Reducing In-Process Inventory Jim Wells, vice-president for manufacturing of the Northern Airplane Company, is exasperated. His walk through the company's most important plant this morning has left him in a foul mood. However, he now can vent his temper at Jerry Carstairs, the plant's production manager, who has just been summoned to Jim's office. "Jerry, I just got back from walking through the plant, and I am very upset." "What is the problem, Jim?" "Well, you know how much I have been emphasizing the need to cut down on our in-process inventory." "Yes, we've been working hard on that," responds Jerry. "Well, not hard enough!" Jim raises his voice even higher. "Do you know what I found by the presses?" "No." "Five metal sheets still waiting to be formed into wing sections. And then, right next door at the inspection station, 13 wing sections. The inspector was inspecting one of them, but the other 12 were just sitting there. You know we have a couple hundred thousand dollars tied up in each of those wing sections. So between the presses and the inspection station, we have a few million bucks worth of terribly expensive metal just sitting there. We can't have that!" The chagrined Jerry Carstairs tries to respond. "Yes, Jim, I am well aware that that inspection station is a bottleneck. It usually isn't nearly as bad as you found it this morning, but it is a bottleneck. Much less so for the presses. You really caught us on a bad morning." "I sure hope so," retorts Jim, but you need to prevent anything nearly this bad happening even occasionally. What do you propose to do about it?" Jerry now brightens noticeably in his response. "Well actually, I've already been working on this problem. I have a couple proposals on the table and I have asked an operations research analyst on my staff to analyze these proposals and report back with recommendations." "Great," responds Jim, "glad to see you are on top of the problem. Give this your highest priority and report back to me as soon as possible." "Will do," promises Jerry Here is the problem that Jerry and his OR analyst are addressing. Each of 10 identical presses is being used to form wing sections out of large sheets of specially processed metal. The sheets arrive randomly to the group of presses at a mean rate of 7 per hour. The time required by a press to form a wing section out of a metal sheet has an exponential distribution with a mean of 1 hour. When finished, the wing sections arrive randomly at an inspection station at the same mean rate as the metal sheets arrived at the presses (7 per hour). A single inspector has the full-time job of inspecting these wing sections to make sure they meet specifications. Each inspection takes her 7 % minutes, so she can inspect 8 wing sections per hour. This inspection rate has resulted in a substantial average amount of in-process inventory at the inspection station (i.e., the average number of wing sheets waiting to complete inspection is fairly large), in addition to that already found at the group of machines. MacRook Pro wang summoned to Jim's office. Jerry, I just got back from walking through the plant, and I am very upset." "What is the problem, Jim?" "Well, you know how much I have been emphasizing the need to cut down on our in-process inventory." "Yes, we've been working hard on that," responds Jerry. "Well, not hard enough!" Jim raises his voice even higher. "Do you know what I found by the presses?" "No." "Five metal sheets still waiting to be formed into wing sections. And then, right next door at the inspection station, 13 wing sections. The inspector was inspecting one of them, but the other 12 were just sitting there. You know we have a couple hundred thousand dollars tied up in each of those wing sections. So between the presses and the inspection station, we have a few million bucks worth of terribly expensive metal just sitting there. We can't have that!" The chagrined Jerry Carstairs tries to respond. "Yes, Jim, I am well aware that that inspection station is a bottleneck. It usually isn't nearly as bad as you found it this morning, but it is a bottleneck. Much less so for the presses. You really caught us on a bad morning." "I sure hope so," retorts Jim, "but you need to prevent anything nearly this bad happening even occasionally. What do you propose to do about it?" Jerry now brightens noticeably in his response. "Well actually, I've already been working on this problem. I have a couple proposals on the table and I have asked an operations research analyst on my staff to analyze these proposals and report back with recommendations." "Great," responds Jim, glad to see you are on top of the problem. Give this your highest priority and report back to me as soon as possible." "Will do," promises Jerry. Here is the problem that Jerry and his OR analyst are addressing. Each of 10 identical presses is being used to form wing sections out of large sheets of specially processed metal. The sheets arrive randomly to the group of presses at a mean rate of 7 per hour. The time required by a press to form a wing section out of a metal sheet has an exponential distribution with a mean of 1 hour. When finished, the wing sections arrive randomly at an inspection station at the same mean rate as the metal sheets arrived at the presses (7 per hour). A single inspector has the full-time job of inspecting these wing sections to make sure they meet specifications. Each inspection takes her 7 % minutes, so she can inspect 8 wing sections per hour. This inspection rate has resulted in a substantial average amount of in-process inventory at the inspection station (i.e., the average number of wing sheets waiting to complete inspection is fairly large), in addition to that already found at the group of machines. The cost of this in-process inventory is estimated to be $8 per hour for each metal sheet at the presses or each wing section at the inspection station. Therefore, Jerry Carstairs has made three alternative proposals to reduce the average level of in-process inventory. Proposal 1 is to use slightly less power for the presses (which would increase their average time to form a wing section to 1.2 hours), so that the inspector can keep up with their output better. This also would reduce the cost of the power for running each machine from $7.00 to $6.50 per hour. The arrival rate for the inspection station would not change and it's still 7 per hour. Proposal 2 is use more power for the presses. This would increase the cost of the power for running each machine to $7.50 per hour while decreasing the average time to form a wing section to 0.8 hour. Again, this would not change the arrival rate for the inspection station. Proposal 3 is to substitute a certain inspector for this task. He is somewhat faster, so he should keep up better. His inspection time would have an exponential distribution with a mean of 7 minutes. This inspector is in a job classification that calls for a total compensation (including benefits) of $19 per hour, whereas the current inspector is in a lower job classification where the compensation is $17 per hour. You are the OR analyst on Jerry carstair's staff who has been asked to analyze this problem. He wants you to "use the latest OR techniques to see how much each proposal would cut down on in-process inventory and then make your recommendations." (a) To provide a basis of comparison, begin by evaluating the status quo. Determine the expected amount of in-process inventory at the presses and at the inspection station. Then calculate the expected total cost per hour when considering all of the following: the cost of the in- process inventory, the cost of the power for running the presses, and the cost of the inspector. (b) What would be the effect of proposal 1? Why? Make specific comparisons to the results from part (a). Explain this outcome to Jerry Carstairs. (c) Determine the effect of proposal 2. Make specific comparisons to the results from part (a). Explain this outcome to Jerry Carstairs. (d) Do the same analysis for proposal 3. (e) Make your recommendations for reducing the average level of in-process inventory at the inspection station and at the group of machines. Be specific in your recommendations, and support them with quantitative analysis you have done in parts (a) to (d). B D E G H K 1 Template for the M/M/s Queueing Model i = Data 7 1 10 Results L = 7.51737284 L = 0.51737284 NO 000 UN (mean arrival rate) (mean service rate) (# servers) = S = 2 3 4 5 6 7 8 9 10 11 W = 1.07391041 W = 0.07391041 Range Name Cells L G4 Lambda C4 La G5 Mu C5 n F13:F38 PO G13 Pn G13:G38 Rho G10 1 Pr(w>t) = when t = 0.7 Prob(W,>t) = 0.22173 when t= n Time 1 Time2 W 12 13 14 15 16 17 18 19 20 21 C6 C9 C12 G7 G8 00 OULAW Probability 0.16 0.14 0.12 0.1 0.08 0.00 0.04 0.02 0 Fi ALLE 22 Number of Customers in System 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 P. 0 0.00085454 1 0.00598176 21 0.020936151 31 0.04885102 41 0.08548928 5 0.11968499 61 0.13963249 7 0.13963249 8 0.12217843 9 0.09502766 10 0.06651936 11 0.04656356 121 0.03259449 131 0.02281614 14 0.0159713 15 0.01117991 16 0.00782594 171 0.00547816 18 0.00383471 19 0.0026843 201 0.00187901 21 0.00131531 22 0.00092071 23 0.0006445 24 0.00045115 25 0.0003158