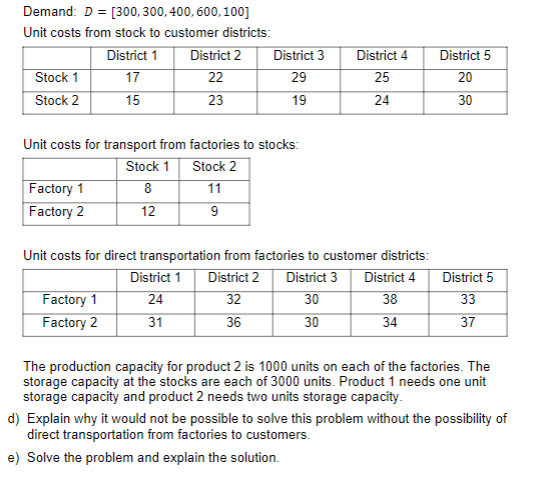
Question: How do you find task d)? Here is the entire Problem. Demand: D = [300, 300, 400,600,100] Unit costs from stock to customer districts: District
How do you find task d)?
Here is the entire Problem.

Demand: D = [300, 300, 400,600,100] Unit costs from stock to customer districts: District 1 District 2 District 3 Stock 1 17 22 29 Stock 2 15 23 19 District 4 25 24 District 5 20 30 Unit costs for transport from factories to stocks: Stock 1 Stock 2 Factory 1 8 11 Factory 2 12 9 Unit costs for direct transportation from factories to customer districts: District 1 District 2 District 3 District 4 Factory 1 24 32 30 38 Factory 2 31 36 34 District 5 33 37 30 The production capacity for product 2 is 1000 units on each of the factories. The storage capacity at the stocks are each of 3000 units. Product 1 needs one unit storage capacity and product 2 needs two units storage capacity d) Explain why it would not be possible to solve this problem without the possibility of direct transportation from factories to customers. e) Solve the problem and explain the solution. Problem 3: We have a transportation problem with two stocks and five customer districts. Both stocks have a capacity of 2000 units and the customer's demand is given as the vector D: D = [500, 700, 600, 1000, 400] The unit costs by transporting from stock to customer is shown in matrix A: District 1 District 2 District 3 District 4 District 5 Stock 1 Stock 2 10 16 13 12 15 20 18 17 14 19 a) Find the optimal solution to the transportation problem, and make a sketch of the solution The two stocks in problem a is served by two factories. Factory 1 has a production capacity of 2000 units and factory 2 has a production capacity of 1500 units during the time horizon The unit costs for transportation from factory to stock is shown in the matrix Stock 1 Stock 2 Factory 1 5 8 Factory 2 6 7 b) Formulate a transshipment model for the distribution problem and find the optimal solution. Make a sketch of the solution and compare it with the result from problem a. In problem b, it is not allowed with direct transportation from factories to districts. If this possibility should be included in the model, we also need the unit costs for transportation directly from factories to customer districts. These costs are shown in the matrix below. Factory 1 Factory 2 District 1 30 26 District 2 32 36 District 3 24 31 District 4 38 34 District 5 30 40 c) Solve this problem to optimality and compare with the solution from problem b. In problem a, b and c, we only had one product. In the next problem, one more product should be introduced Product 1 is similar as in the first problems, while product 2 has the following information attached Demand: D = [300, 300, 400,600,100] Unit costs from stock to customer districts: District 1 District 2 District 3 Stock 1 17 22 29 Stock 2 15 23 19 District 4 25 24 District 5 20 30 Unit costs for transport from factories to stocks: Stock 1 Stock 2 Factory 1 8 11 Factory 2 12 9 Unit costs for direct transportation from factories to customer districts: District 1 District 2 District 3 District 4 Factory 1 24 32 30 38 Factory 2 31 36 34 District 5 33 37 30 The production capacity for product 2 is 1000 units on each of the factories. The storage capacity at the stocks are each of 3000 units. Product 1 needs one unit storage capacity and product 2 needs two units storage capacity d) Explain why it would not be possible to solve this problem without the possibility of direct transportation from factories to customers. e) Solve the problem and explain the solution. Problem 3: We have a transportation problem with two stocks and five customer districts. Both stocks have a capacity of 2000 units and the customer's demand is given as the vector D: D = [500, 700, 600, 1000, 400] The unit costs by transporting from stock to customer is shown in matrix A: District 1 District 2 District 3 District 4 District 5 Stock 1 Stock 2 10 16 13 12 15 20 18 17 14 19 a) Find the optimal solution to the transportation problem, and make a sketch of the solution The two stocks in problem a is served by two factories. Factory 1 has a production capacity of 2000 units and factory 2 has a production capacity of 1500 units during the time horizon The unit costs for transportation from factory to stock is shown in the matrix Stock 1 Stock 2 Factory 1 5 8 Factory 2 6 7 b) Formulate a transshipment model for the distribution problem and find the optimal solution. Make a sketch of the solution and compare it with the result from problem a. In problem b, it is not allowed with direct transportation from factories to districts. If this possibility should be included in the model, we also need the unit costs for transportation directly from factories to customer districts. These costs are shown in the matrix below. Factory 1 Factory 2 District 1 30 26 District 2 32 36 District 3 24 31 District 4 38 34 District 5 30 40 c) Solve this problem to optimality and compare with the solution from problem b. In problem a, b and c, we only had one product. In the next problem, one more product should be introduced Product 1 is similar as in the first problems, while product 2 has the following information attached






