How do you write a recursive function for the following matrix given above which returns the L and U matrix in python?

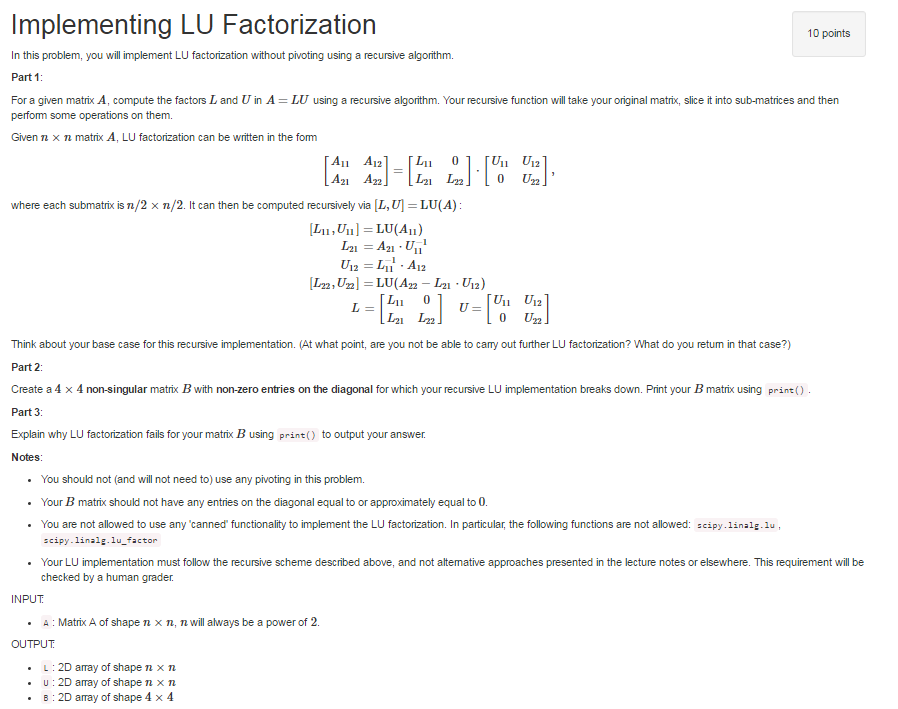
Implementing LU Factorization 10 points In this problem, you will implement LU factorization without pivoting using a recursive algorithm. Part 1 For a given matrix A, compute the factors Land U in A LU using a recursive algorithm. Your recursive function will take your original matrix, slice it into sub-matrices and then perform some operations on them. Given n x n matrix A, LU factorization can be written in the fom 11 A121 TLlu 0 11 12 21 LU(All) 11 12 12 11 LU (A L21 U12) L22, U 11 12 L21 L22 Think about your base case forthis recursive implementation. (At what point, are you not be able to camy out further LU factorization? What do you retum in that case?) Part 2: Create a 4 x 4 non-singular matrix Bwith non-zero entries on the diagonal for which your recursive LU implementation breaks down. Print your Bmatrix using print 0. Part 3 Explain why LU factorization fails for your matrix Busing print to output your answer Notes: You should not (and will not need to) use any pivoting in this problem. Your B matrix should not have any entries on the diagonal equal to orapproximately equal to 0 You are not allowed to use any canned functionality to implement the LU factorization. In particular, the following functions are not allowed scipy.linale.lu lg-1 Py Your LU implementation must follow the recursive scheme described above, and not altemative approaches presented in the lecture notes or elsewhere. This requirement will be checked by a human grader INPUT A: Matrix A of shape n x n, n will always be a power of 2 OUTPUT L 2D amay of shape n x n U 2D amay of shape n x n B 2D array of shape 4 x 4 Implementing LU Factorization 10 points In this problem, you will implement LU factorization without pivoting using a recursive algorithm. Part 1 For a given matrix A, compute the factors Land U in A LU using a recursive algorithm. Your recursive function will take your original matrix, slice it into sub-matrices and then perform some operations on them. Given n x n matrix A, LU factorization can be written in the fom 11 A121 TLlu 0 11 12 21 LU(All) 11 12 12 11 LU (A L21 U12) L22, U 11 12 L21 L22 Think about your base case forthis recursive implementation. (At what point, are you not be able to camy out further LU factorization? What do you retum in that case?) Part 2: Create a 4 x 4 non-singular matrix Bwith non-zero entries on the diagonal for which your recursive LU implementation breaks down. Print your Bmatrix using print 0. Part 3 Explain why LU factorization fails for your matrix Busing print to output your answer Notes: You should not (and will not need to) use any pivoting in this problem. Your B matrix should not have any entries on the diagonal equal to orapproximately equal to 0 You are not allowed to use any canned functionality to implement the LU factorization. In particular, the following functions are not allowed scipy.linale.lu lg-1 Py Your LU implementation must follow the recursive scheme described above, and not altemative approaches presented in the lecture notes or elsewhere. This requirement will be checked by a human grader INPUT A: Matrix A of shape n x n, n will always be a power of 2 OUTPUT L 2D amay of shape n x n U 2D amay of shape n x n B 2D array of shape 4 x 4