Question: How many basic feasible solutions? Assuming the dashed line represent the objective function Z= c1x1+c2x2 and the point E has beter value (larger for max
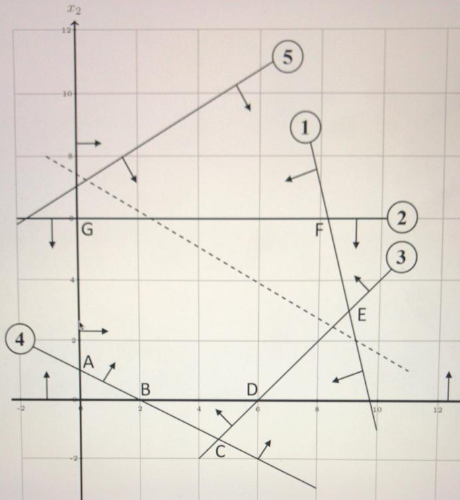
- How many basic feasible solutions?
- Assuming the dashed line represent the objective function Z= c1x1+c2x2 and the point E has beter value (larger for max problem, or smaller for a min problem) than the point G . select the binding constraints
- Assuming the dashed line represent the objective function Z= c1x1+c2x2 and the point E has beter value (larger for max problem, or smaller for a min problem) than the point G .
Which point gives the optimal solution? select answer
- F
- A
- There is infinite number of optimal solution from A to B
- More information is needed to answer this question
- Assuming the dashed line represent the objective function and the point E has better value (larger for max problem, or smaller for a min problem) than the point G. removing constraint 3 will change the optimal solution
- True
- False
- Assuming the dashed line represent the objective function Z= c1x1+c2x2 and the point F gives the optimal solution. Select all statement that can be said about the point (0,4) where and .
- It is a feasible solution
- It can be written as convex combination of point between A and B.
- It is basic feasible solution
- It is basic solution
- Assuming the dashed line represent the objective function Z= c1x1+c2x2 and the point F gives the optimal solution. Select all statement that can be said about the point (2,4) where x1=2 and x2=4.
- It can be written as convex combination of the basic feasible solutions
- It gives better z-value some basic feasible solutions
- It gives better z-value than point (0,4)
- It is extreme point
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


