Question: How many integer solutions are there to the equation: $1+$2+$3+$4= 16? Score: 011 3 Unanswered Advice The number of different solutions to this equation is

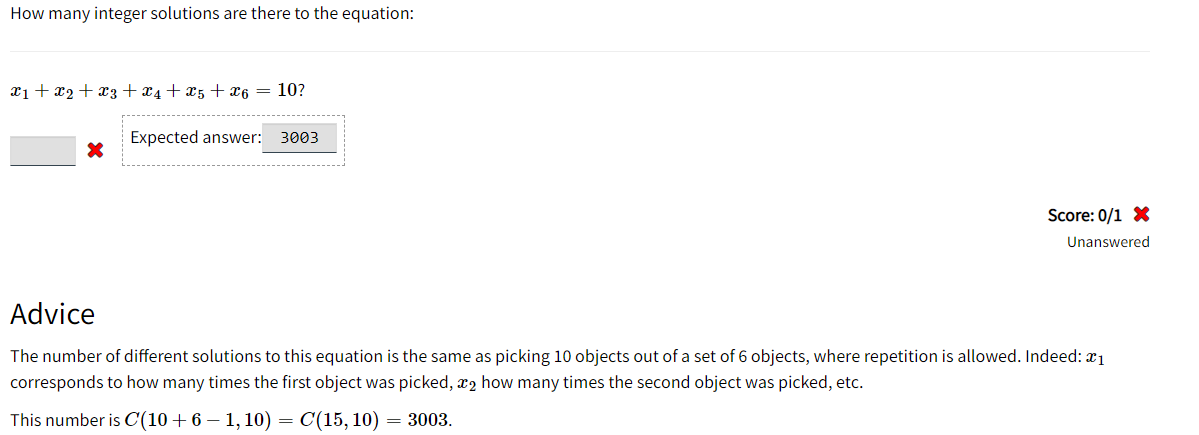
How many integer solutions are there to the equation: $1+$2+$3+$4= 16? Score: 011 3 Unanswered Advice The number of different solutions to this equation is the same as picking 16 objects out of a set of4 objects, where repetition is allowed. Indeed: 1:1 corresponds to how many times the first object was picked,x2 how many times the second object was picked, etc. This number is C(l + 4 l, 16) = C(19,16) = 969. How many integer solutions are there to the equation: x1+2+ 23 + 24 + 25+ 26 = 10? Expected answer: 3003 X Score: 0/1 X Unanswered Advice The number of different solutions to this equation is the same as picking 10 objects out of a set of 6 objects, where repetition is allowed. Indeed: x1 corresponds to how many times the first object was picked, x2 how many times the second object was picked, etc. This number is C(10 + 6 - 1, 10) = C(15, 10) = 3003

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Hello, I havetwo articles about S Corp. and C Corp., and IJUST need towrite a conclusion paragraph based on professor's questions. can you help me to write it? Articles are attached Accounting...

What is the prime factorisation of a = 43560? a=22.32.53.11 O a=2.33.52.112 O a=2.32.52.113 O a=22.32.5-113 O a=23.32.52.11 O a=23.32.5-112 What is the prime factorisation of b=24750? O b=2.32.53.11...

Exercise 1. a) How many committees of 3 people can be formed from a pool of 15 people? b) In how many ways we can form a group of 3 people to serve as a president, vice president and secretary for a...

QUESTION 1 How many 7-digit phone numbers are there wherein the digits are non-decreasing (.e. every digit is greater than or equal to the one prior)? Answer: > > QUESTION 2 How many integer...

Let a, b, c be non-zero integers. Prove that if ar + by = c has an integer solution, then at least one of the following is true: . ar + by = c has infinitely many integer solutions (r, y) where r is...

How many integer solutions are there to the equation a + b + c = 13 (where the values of a, b, and c are all greater than 0)? Answer: How many integer solutions are there to the equation a + b +C+ d...

20. Find the number of seven digit positive integers such that the sum of the digits is 19. 21. In how many ways is it possible to separate the nine letters a, b, c, d, e, f, g, h, i into three non...

5. This final question will walk us through the solutions (or lack thereof) to the linear diophantine equations 3n + 6m = 1 and 3n + 5m = 1. (a) Prove the following theorem: Theorem. There do not...

The earned income credit aCannot exceed the amount of the tax liability bIs available to married taxpayers who file separate returns cIs available only if the taxpayer has qualifying children dMust...

Write a paper about IT sourcing strategies in which summarize each article related to the IT sourcing strategies and compare and contrast the sourcing approaches in each article. Identify the factors...

Item 9 Time Remaining 2 hours 4 8 minutes 1 6 seconds 0 2 : 4 8 : 1 6 Item 9 Time Remaining 2 hours 4 8 minutes 1 6 seconds 0 2 : 4 8 : 1 6 Oakley is the CFO for Parsons Project Management. They have...

The following account balances come from the records of Teton Company. Account Beginning Balance Ending Balance Accounts Receivable $2,580 $3,821 Allowance for Doubtful Accounts 131 195 During the...