how this number is normalized !

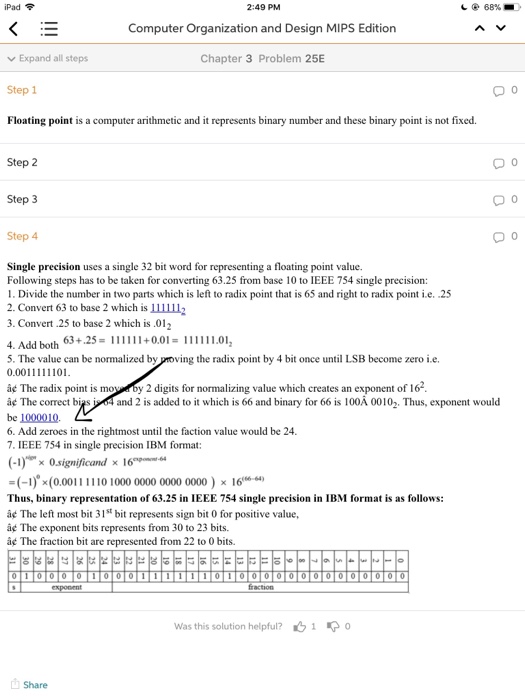
iPad 2:49 PM Computer Organization and Design MIPS Edition Chapter 3 Problem 25E 68%- v Expand all steps Step 1 Floating point is a computer arithmetic and it represents binary number and these binary point is not fixed. 0 0 Step 2 Step 3 Step 4 0 Single precision uses a single 32 bit word for representing a floating point value. Following steps has to be taken for converting 63.25 from base 10 to IEEE 754 single precision: 1. Divide the number in two parts which is left to radix point that is 65 and right to radix point i.e. .25 2. Convert 63 to base 2 which is lll1l 3. Convert.25 to base 2 which is .012 5. The value can be normalized by oving the radix point by 4 bit once until LSB become zero i.e ae The radix point is mov by 2 digits for normalizing value which creates an exponent of 16 at The correct b be 1000010. 6. Add zeroes in the rightmost until the faction value would be 24. 7. IEEE 754 in single precision IBM format: and 2 is added to it which is 66 and binary for 66 is 100A 00102. Thus, exponent would (-)x(0.0011 1110 1000 0000 0000 0000) x 16 4 Thus, binary representation of 63.25 in IEEE 754 single precision in IBM format is as follows: e The left most bit 31st bit represents sign bit 0 for positive value, ac The exponent bits represents from 30 to 23 bits. ae The fraction bit are represented from 22 to 0 bits. Was this solution helpful? 1 0 Share