How to solve this question?

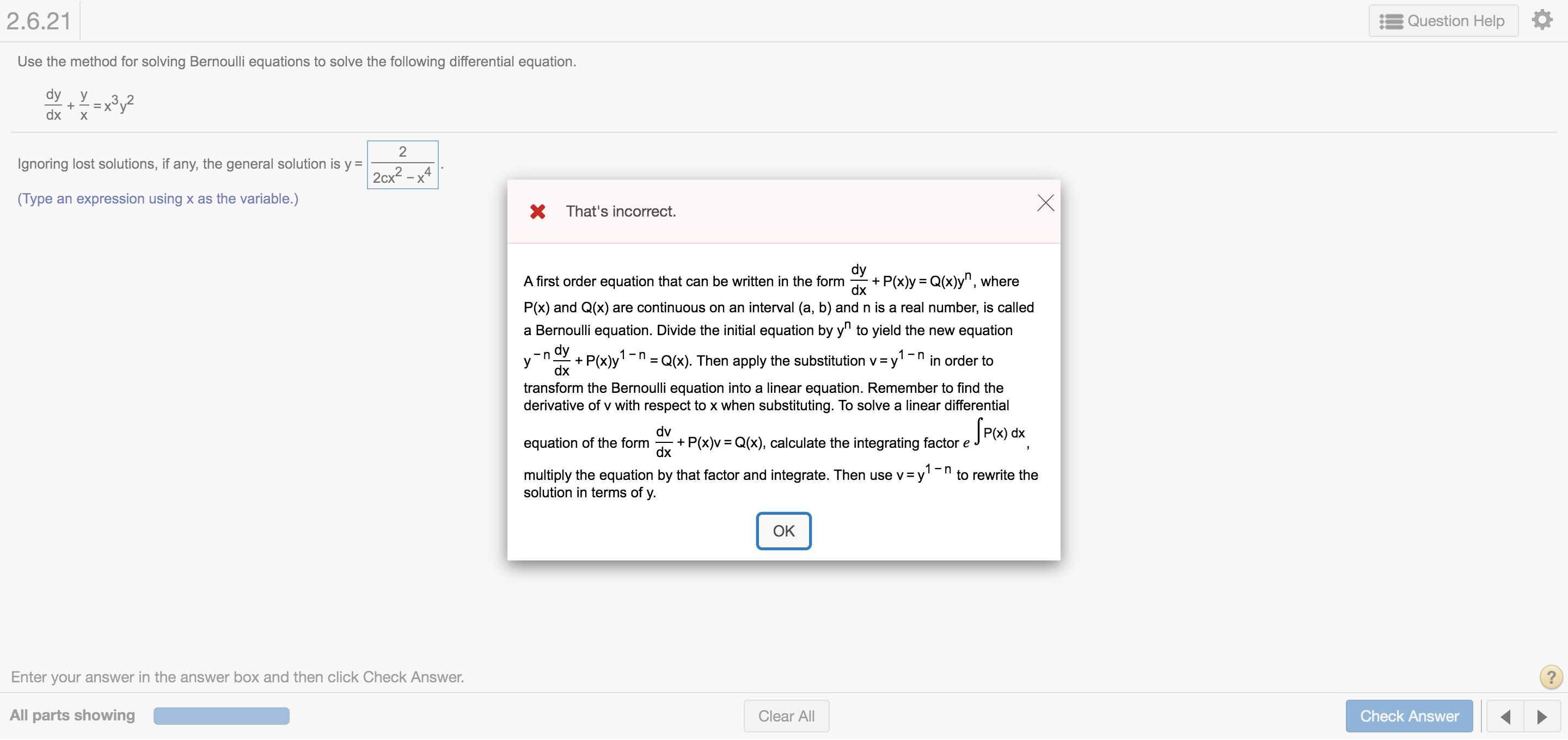
2.6.21 Use the method for solving Bernoulli equations to solve the following differential equation. Ignoring lost solutions. if any. the general solution is y = (Type an expression using x as the variable.) Enter your answer in the answer box and then click Check Answer. All parts showing x That's incorrect. d A rst order equation that can be written in the form d: + P(x)y = Q(x)y", where P(x) and Q(x) are continuous on an interval (a. b) and n is a real number, is called a Bernoulli equation. Divide the initial equation by y" to yield the new equation _ d _ _ y "i + P(x)y'1 n = Q(x). Then apply the substitution v =y1 " in order to transform the Bernoulli equation into a linear equation. Remember to nd the derivative of v with respect to x when substituting. To solve a linear dierential IP(x) dx dv equation of the form a 4- P(X)V = Q(x). calculate the integrating factor 9 multiply the equation by that factor and integrate. Then use v= y'1 _ " to rewrite the solution in terms of y. Clear All EE Question Help a CheckAnswer ' 1 b