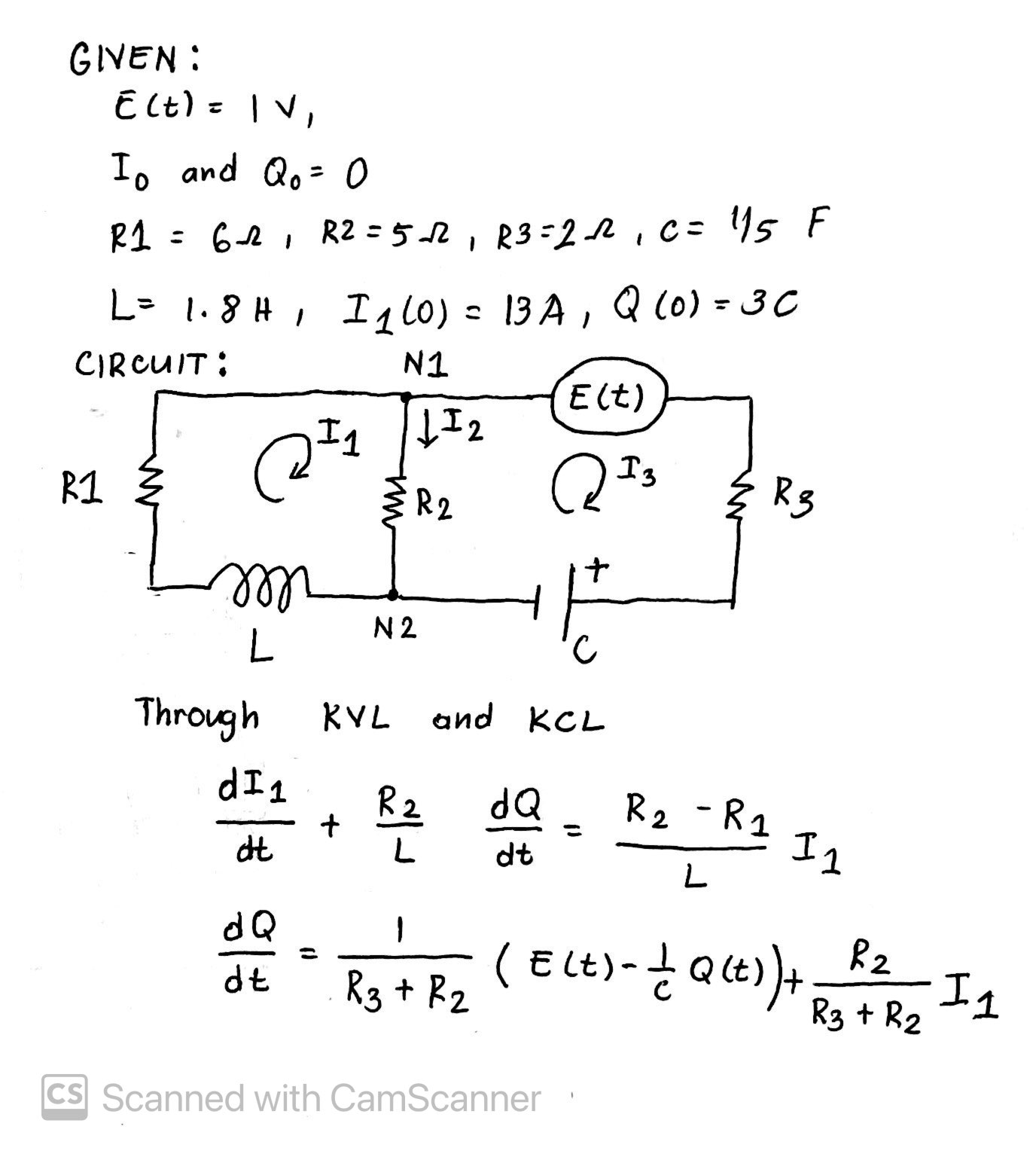
Question: How to solve this RLC Circuit through differential equations using Laplace Transform? E(t) is the alternating voltage. I already got the differential equations through Kirchhoff's

How to solve this RLC Circuit through differential equations using Laplace Transform?

E(t) is the alternating voltage. I already got the differential equations through Kirchhoff's Voltage and Current Law, but I'm kind of stuck. Provide explanation and sol'n pls! Thanks.

GIVEN : E(t ) = IV, Io and Qo = 0 R1 = 6 2 1 R2 = 5 12 , R3 = 2 2 , C= 1/5 F L = 1 . 8 H , I1 (0 ) = 13 A , Q (0) = 30 CIRCUIT : N1 E(t) 1I2 R1 3 R 2 QIs R3 + N 2 L Through KVL and KCL dI1 + R 2 dQ - R2 - R 1 de L dt : I1 L dQ dt R3 + R2 ( ELt ) - - Q (t) ) + R2 R3 + R2 I1 CS Scanned with CamScanner

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Math 1152 Project #4 Solving Initial Value Problems using Power Series and the Laplace Transform Due: Tuesday, April 11 Name(s): - - - - - - - - - - - - - - - - - - - - Description - - - - - - - - -...

Please adapt the given MATLAB script to solve the problem Project 6.2 Figure P6.2a shows a third-order RLC circuit. To run a time-domain transient anal- ysis, we transform the ci rcuit into...

Learning Goal: To use Laplace transform concepts to transform any circuit from the time domain to the s - domain. We develop a general technique for analyzing the complete response of any linear...

MATLAB Calculating voltage using Kirchhoff loops 0 solutions submitted (max: Unlimited) This example demonstrates assessing correctness by checking the value of variables in the student solution. The...

please answer questions using figure 3a ,3b Q3) Figure Q3 (a) illustrates a solenoid with a retum spring. (Total mark =40\%) Figure Q3(a) The voltage v(t) across the winding. causes a current u(t) to...

Need Help with Computational Physics HW for python on calculating electrostatic potential. Book from Computational physics by mark newman Need it solved in Overrelaxation method: Exercise 9.3: V 0...

please to write matlab code. Objective: To gain experience in using MATLAB as a programming language. To use MATLAB to simulate the response of electrical circuits. Background: The behavior of the...

Can you help me fix this problem, please? MAT330ProjectOne Template.mlx x + /MATLAB Drive/MAT330ProjectOneTemplate.mix figure(4) 51 R = 100; 52 L = 5; 53 C = 1/450500; 54 55 ode = strcat('d2V/dt2 +...

Please solve the project in MATLAB Project 6.2 Figure P6.2a shows a third-order RLC circuit. To run a time-domain transient anal- ysis, we transform the ci rcuit into differential equations using the...

On December 31, Rogers Company had the following list of account balances. 0 Accounts Payable Accounts Receivable Accumulated Depreciation. Buildings Accumulated Depreciation, 0 Buipment DBeginning...

Our firm is considering the purchase of a new inventory management system, which is anticipated to cost $1,150,000. The system will be depreciated using the five year MACRS depreciation method (see...

Which one of the following is the systematic risk in Agriculture? Group of answer choices Pest problems Trade wars Internal HR issues Farm succession problems

1. What is the coefficient of x4 in the Taylor Series for the function f(x) = cos x about x = 0? 00 2. If the function f is defined by f(x): = x3n then f'(x) = = ? Write the first four nonzero terms...