how to solve using python

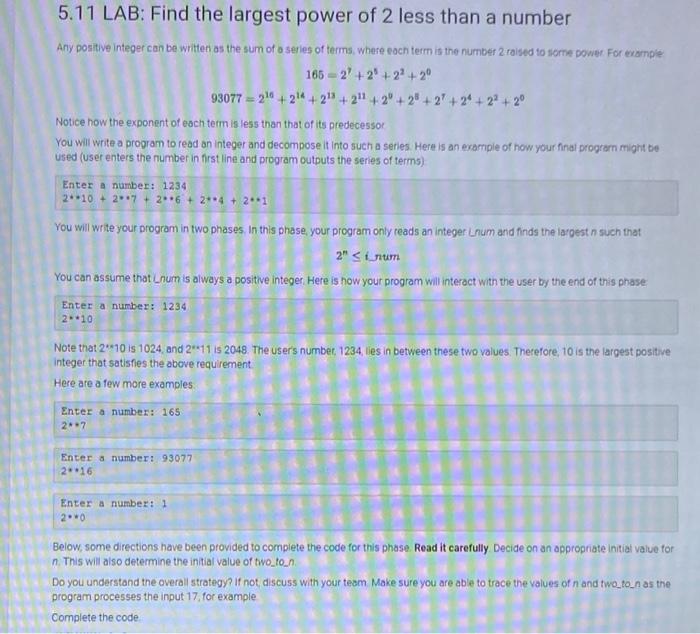
5.11 LAB: Find the largest power of 2 less than a number Any positive integer can be written as the sum of o series of terms, where each term is the number 2 raised to some power. For evample 165=27+26+22+2093077=210+214+213+211+20+25+27+24+22+20 Notice how the exponent of each term is less than that of its predecessor You will write a program to read an integer and decompose it into such a series. Here is an example of how your final program might be used (user enters the number in first line and program outputs the series of terms) Enter a number: 1234 210+27+26+24+2+1 You will write your program in two phases, In this phase, your program only reads an integer Lnum and finds the largest n such that 2n1num You can assume that Lnum is always a positive integer Here is how your program will interact with the user by the end of this phase: Enter a number: 1234 2+10 Note that 210 is 1024, and 211 is 2048. The user's number, 1234 , lies in between these two values. Therefore, 10 is the largest positive integer that satisfes the above requirement. Here are a few more examples: Enter a number: 165 2+7 Encer a number: 93077 2+16 Enter a number: 1 20 Below, some directions have been provided to complete the code for this phase. Read it carefully Decide on an appropriate initial value for n. This will also determine the initial value of two_to n. Do you understand the overall strategy? if not, discuss with your team Make sure you are able to trace the values of n and two to n as the program processes the input 17, for example Complete the code