How would I solve problem 3 by hand given the following information?

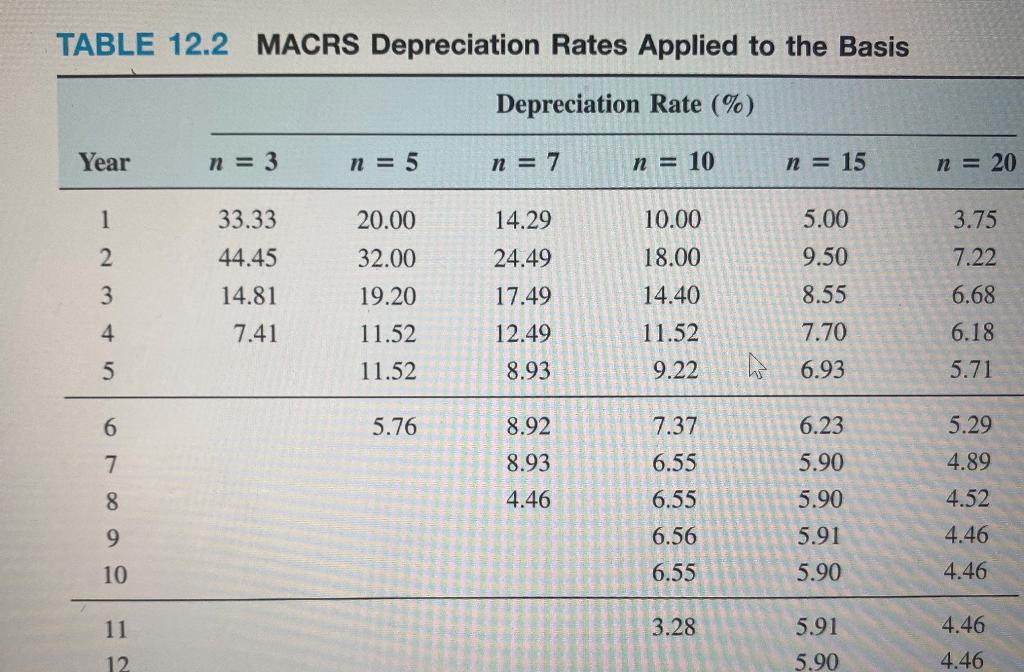
3. (12.34) To determine the MACRS rates in Table 12.2, the switching procedure in Section 12.5 must be altered slightly to accommodate the half-year convention imposed by MACRS. The first difference is in year 1, where the DDB rate is only one-half of the DDB rate. The second difference is in the denominator for the SL depreciation. The term is (n - t + 1.5), instead of the (n - t + 1) shown. The third and final change is that one-half of the SL depreciation allowed in year n is taken in the year n + 1. Use this procedure and three changes to verify the MACRS rates for n = 5. (20points) 12.5 TAX DEPRECIATION SYSTEM IN CANADA In most industrialized countries, depreciation is based on classical methods SL, DDB, and others. Some countries require a standardized form of depreciation for tax purposes, much like the United States uses MACRS. Canada is a good exam- ple. It uses a system called CCA (Capitalized Cost Allowance), which has as a foundation the declining balance method. The CCA system prescribes only a fixed annual rate of write-off (the CCA rate), rather than the recovery period and a varying annual rate of depreciation like the MACRS rates. The annual CCA depre- ciation and book value, which is termed UCC (Undepreciated Capital Cost) are calculated using relations similar in several respects to the DB and MACRS meth- ods. Additionally, only 50% of the first year's CCA can be claimed, thus prevent- ing the purchase of depreciable assets at the end of the fiscal year and claiming an entire year's CCA charge. For years t = 1, 2, ... and basis B, the CCA and UCC are calculated as follows. S = 0.5(CCA rate)B t = 1 = (CCA rate)UCC,-1 t = 2, 3, ... , { j=1 CCA ; , UCC, = B - t = 1, 2, ... j=1 It is easy to conclude that the relation for CCA is very similar to the DB method's annual depreciation, Equation [12.5]. The UCC relation is the same as the BV rela- tion for any depreciation method, namely, the basis minus all accumulated depre- ciation to date. TABLE 12.2 MACRS Depreciation Rates Applied to the Basis Depreciation Rate (%) Year n = 3 n = 5 n = 7 n = 10 n = 15 n = 20 1 33.33 20.00 5.00 2 44.45 14.81 32.00 19.20 11.52 14.29 24.49 17.49 12.49 8.93 10.00 18.00 14.40 3 3.75 7.22 6.68 9.50 8.55 7.70 4 7.41 6.18 11.52 9.22 5 11.52 th 6.93 5.71 6 5.76 7.37 5.29 7. 8.92 8.93 4.46 6.55 6.55 6.23 5.90 5.90 5.91 4.89 4.52 8 9 6.56 4.46 10 6.55 5.90 4.46 11 3.28 5.91 5.90 4.46 4.46 12 3. (12.34) To determine the MACRS rates in Table 12.2, the switching procedure in Section 12.5 must be altered slightly to accommodate the half-year convention imposed by MACRS. The first difference is in year 1, where the DDB rate is only one-half of the DDB rate. The second difference is in the denominator for the SL depreciation. The term is (n - t + 1.5), instead of the (n - t + 1) shown. The third and final change is that one-half of the SL depreciation allowed in year n is taken in the year n + 1. Use this procedure and three changes to verify the MACRS rates for n = 5. (20points) 12.5 TAX DEPRECIATION SYSTEM IN CANADA In most industrialized countries, depreciation is based on classical methods SL, DDB, and others. Some countries require a standardized form of depreciation for tax purposes, much like the United States uses MACRS. Canada is a good exam- ple. It uses a system called CCA (Capitalized Cost Allowance), which has as a foundation the declining balance method. The CCA system prescribes only a fixed annual rate of write-off (the CCA rate), rather than the recovery period and a varying annual rate of depreciation like the MACRS rates. The annual CCA depre- ciation and book value, which is termed UCC (Undepreciated Capital Cost) are calculated using relations similar in several respects to the DB and MACRS meth- ods. Additionally, only 50% of the first year's CCA can be claimed, thus prevent- ing the purchase of depreciable assets at the end of the fiscal year and claiming an entire year's CCA charge. For years t = 1, 2, ... and basis B, the CCA and UCC are calculated as follows. S = 0.5(CCA rate)B t = 1 = (CCA rate)UCC,-1 t = 2, 3, ... , { j=1 CCA ; , UCC, = B - t = 1, 2, ... j=1 It is easy to conclude that the relation for CCA is very similar to the DB method's annual depreciation, Equation [12.5]. The UCC relation is the same as the BV rela- tion for any depreciation method, namely, the basis minus all accumulated depre- ciation to date. TABLE 12.2 MACRS Depreciation Rates Applied to the Basis Depreciation Rate (%) Year n = 3 n = 5 n = 7 n = 10 n = 15 n = 20 1 33.33 20.00 5.00 2 44.45 14.81 32.00 19.20 11.52 14.29 24.49 17.49 12.49 8.93 10.00 18.00 14.40 3 3.75 7.22 6.68 9.50 8.55 7.70 4 7.41 6.18 11.52 9.22 5 11.52 th 6.93 5.71 6 5.76 7.37 5.29 7. 8.92 8.93 4.46 6.55 6.55 6.23 5.90 5.90 5.91 4.89 4.52 8 9 6.56 4.46 10 6.55 5.90 4.46 11 3.28 5.91 5.90 4.46 4.46 12