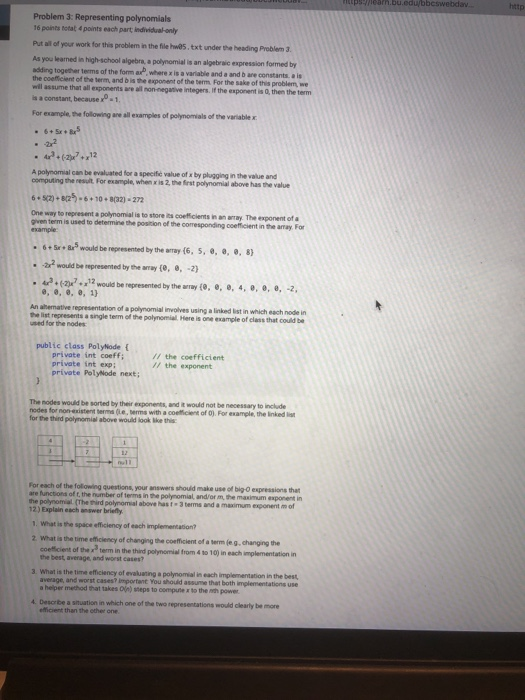
http Problem 3: Representing polynomials 16 points totat 4 points each part lndividualtonly Put all of your work for this problem in the file hwa5.txt under the heading Problem 3. As you kearned in high school algebra a polynomial is an algebraic esxpression formed by adding together terms of the form ax where xis a variable and a and b are constants. is the coefficient of the term, and b is the exponent of the term For the sake of this problem, we exponents are all non-negantive integers. If the exponent is Q, then the term is a constant, because 1 For example, the following ane all lexamples of polymomials of the variable x polynomial can be evaluated for a specific value of x by plugging in the value and computing the result, For example, when x is 2, the first polynomial above has the value 62)+825-6+10 8(32)-272 One way to represent a polynomial is to store its coefficients in an aay The exponent of a term is used to determine the position of the comesponding coefficient in the array For 6+5r+ 8k5 would be repeesented by the array (6, 5, , a, , 8) 2x2 would be represented by the aray te, , 2) 4(2.12 would be represented by the aray (e, e, e, 4, e, , e, 2, e, e, e, e, 1 An ahermative representation of a polynomial involves using a linked list in which each node in the list represents a single term of the polymomial Here is one example of class that could be used for the public class PolyNode private int coeffi the exponent private int exp private PolyNode next; // the coefficient The nodes would be sorted by their exponents, and it would not be necessary to inckude nodes for non existent erms (Le, terms with a coefficient of 0). For example, the inked lst for the third polymomial above would look lke this For each of the following questions, your answers should make use of big-O expressions that terms in the polymomial and/or m the maximum exponent in are functions of t, the number of he polmomial (The rird ponmomial above has t - 3 terms and a masimum exponent m of t 12) Explain each answer briefly . What is the space efficlency of each implementation? 2 What is the time etficieney of changing the coeficient of a serm (ie g.changing the coeficient of the 2 term in the thind potymomial from 4 10 10) in each implementation the best, average, and worst cases 3. What is the time efficiency of evaluaning a pohnomial in each implementation in the best average, and worst cases? important You should assume that both impiementations use aheper method that takes n) steps to compune x to the er orbe a shuation in which one of the two representations would clearly be more efficient than the other one 4 Des