https://drive.google.com/file/d/0ByYI8v2Q1ZBTZDFpQW5RZWlMQ0k/view?usp=sharing

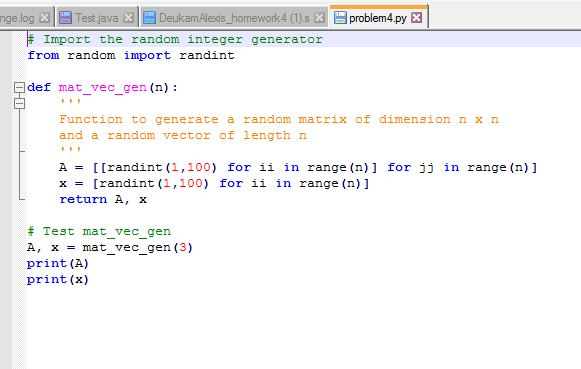
# Import the random integer generator

from random import randint

def mat_vec_gen(n):

'''

Function to generate a random matrix of dimension n x n

and a random vector of length n

'''

A = [[randint(1,100) for ii in range(n)] for jj in range(n)]

x = [randint(1,100) for ii in range(n)]

return A, x

# Test mat_vec_gen

A, x = mat_vec_gen(3)

print(A)

print(x)

In class, we talked about matrix-vector multiplication and the time complexity of algorithms. This problem will integrate these topics as wel as give you a first-hand encounter with time complexity ayou will find a file called problem4.py containing a function called mat.vec-gen.py. This function takes in an integer argument n and generates a random nx n matrix and length-n vector. The vector is stored as a Python list, and the matrix is stored as a Python list-of-lists, which each sublist corresponding to a row in the matrix. Al you l find tutorials describing how to plot graphs and record timing estimates in Python (available as a Jupyter notebook and here as a PDF file. If your native Python distribution does not contain plotting and timing routines, it is highly recommended that you downmload and install the Anaconda 3.6 distribution of Python (a) Write a function called mat.vec) that takes as input a square matrix and a vector of compatible dimensions, and returns the resulting product vector. That is, if the input are an n n matrix A and an n 1 vector x, then mat-vec (A, x)= Ax. Test your function on small matrices and vectors that you can check by hand. When you are satisfied, move on to parts (b) and (c). Additionally print out your code for this function and include it with your assignment (b) We saw that the complexity of matrix-vector multiplication is O(n2). Use your mat.vec) function and record the time needed to multiply an n n matrix by a vector of length n, for n sizes 10, 20,40, 80, 160, 320,640, 1280, 2560, 5120, 10240]. Store these timing estimates in a list (say, timing). Create a plot of the matrix sizes (sizes) on the horizontal axis versus the run-times to perform the multiplications (timing) on the vertical axis. Be sure to label your axes! Include a print-out of this plot with your assignment. Write a sentence or two about whether or not the shape of this plot matches your expectations based on the complexity of matrix-vector multiplication (c) Compute the ratios of timings for consecutive matrix/vector sizes and store them in the list ratios Specifically, ratios [i] timings [i+1]/timings[i]. Print out the list and include it with your assignment. Write a sentence or two about whether or not the values of these ratios match your expectations based on the complexity of matrix-vector multiplication. You may find it helpful to make a plot of ratios as a function of sizes, but this is not required