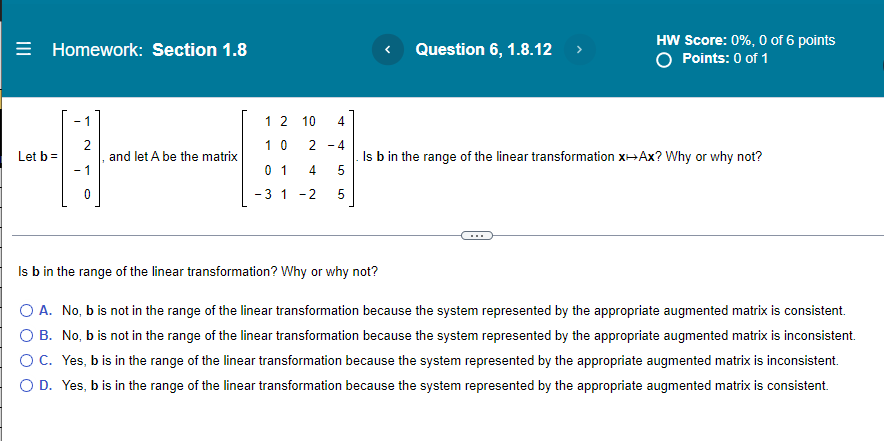
HW Score: 0%, E] of E- points 0 Points: [I of 1 Homework: Section 1.8 Question 5, 1.8.11 1 1 4 4 4 Let b= 1 . and letAbe the matrix 0 1 3 4 . Is I: in the range of the linear transformation a: I> Ax? Why or why not? 0 2 B 2 3 Is b in the range of the linear transformation? Why or why not\"? C) A. No, b is not in The range of The linear transformation because the system represented by the augmented matrix [A b] is inconsistent. O B. No. b is not in The range of The linear transformation because the system represented by the augmented matrix [A b] is consistent. Cl C. Yes, I] is in The range of The linear transformation because the system represented by the augmented matrix [A b] is inconsistent. O D. Yes, I] is in The range of The linear transformation because the system represented by the augmented matrix [A b] is consistent. E Homework: Section 1.8 HW Score: 0%, 0 of 6 points O Points: 0 of 1 1 2 10 4 2 10 2 -4 Let b = and let A be the matrix . Is b in the range of the linear transformation xAx? Why or why not? 1 0 1 4 5 -3 1 -2 5 Is b in the range of the linear transformation? Why or why not? O A. No, b is not in the range of the linear transformation because the system represented by the appropriate augmented matrix is consistent. O B. No, b is not in the range of the linear transformation because the system represented by the appropriate augmented matrix is inconsistent. O C. Yes, b is in the range of the linear transformation because the system represented by the appropriate augmented matrix is inconsistent. O D. Yes, b is in the range of the linear transformation because the system represented by the appropriate augmented matrix is consistent