I already have the code written. I just need detailed explanation.

What is the ratio of the areas of the inscribed circle to that of the unit square?

If we pick a random point within the unit square what is the probability that the point will also lie within the circle?

If we repeat this experiment an arbitrarily large number of times the ratio of the number of points which lie within the circle to the number of points within the unit square (all of them) will approach ?/4.

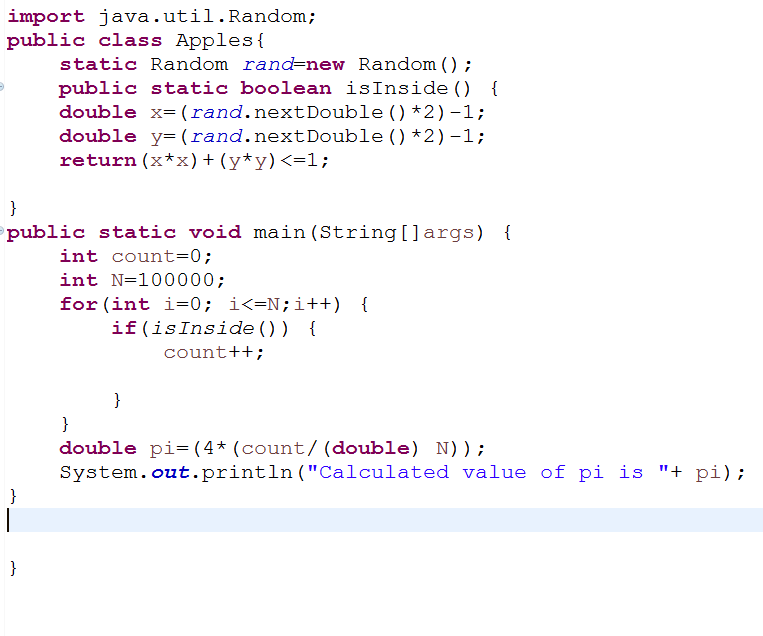
Using the language structures we have discussed write a program that will do the above experiment an arbitrary (determined at run-time) number of times and report back the approximate value of ?. **PLEASE EXPLAIN 1. WHY THE PI= (4*(count/(double) N));**

2. return(x*x)+(y*y)

3. double x=(rand.nextDouble()*2) -1;

Thank you for the hard work.

mport java.util.Random; public class Applesf static Random rand-new Random ); public static boolean isInside ) double x= (rand. nextDouble()*2)-1; double y (rand.cxiDonlbl () k2) 1. return (x*x) + (yty) =1; public static void main (String[]args) t int count-0; int N=100000; for (int 1-0; i