Question: I already have the solution to this question. I need a step-by-step walkthrough with help understanding it. How do you: 1)Replace the right-hand side of
I already have the solution to this question. I need a step-by-step walkthrough with help understanding it.
How do you: 1)Replace the right-hand side of your differential equation with 0 to make a homogeneous equation?
2) Write the auxiliary equation for this homogeneous second-order linear differential equation?
3)Solve the auxiliary equation.
4)Based on the solution(s) of the auxiliary equation, what is the general solution for the homogeneous differential equation, .
5)Does any of the terms from the homogeneous solution match terms from the right-hand side of the original differential equation?
If so, this will require an extra factor of the independent variable to be included with the basic set-up of the particular solution.
6) What is the basic set-up, using undetermined coefficients, for the particular solution of the non-homogeneous differential equation?
7)Plug this basic solution into this differential equation and solve for the undetermined coefficients. What is the particular solution, , after all coefficients have been determined?
8)The general solution for a non-homogeneous differential equation can be found by combining the homogeneous and the particular solutions. What is the general solution of this differential equation?
9)Use the general solution and the initial conditions to solve for the values of any arbitrary constants.
10) The solution for the initial value problem will be the general solution, with the arbitrary constants replaced with their actual values. What is the solution of the initial value problem (is that what is listed below?
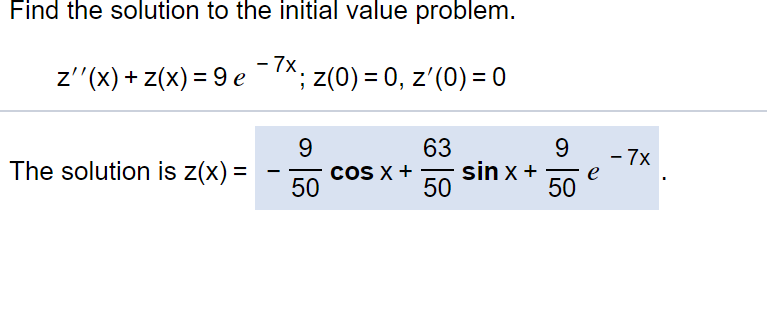
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


