I am having trouble solving the question and don't know the steps or how to start. Can I get the answer in a written solution?

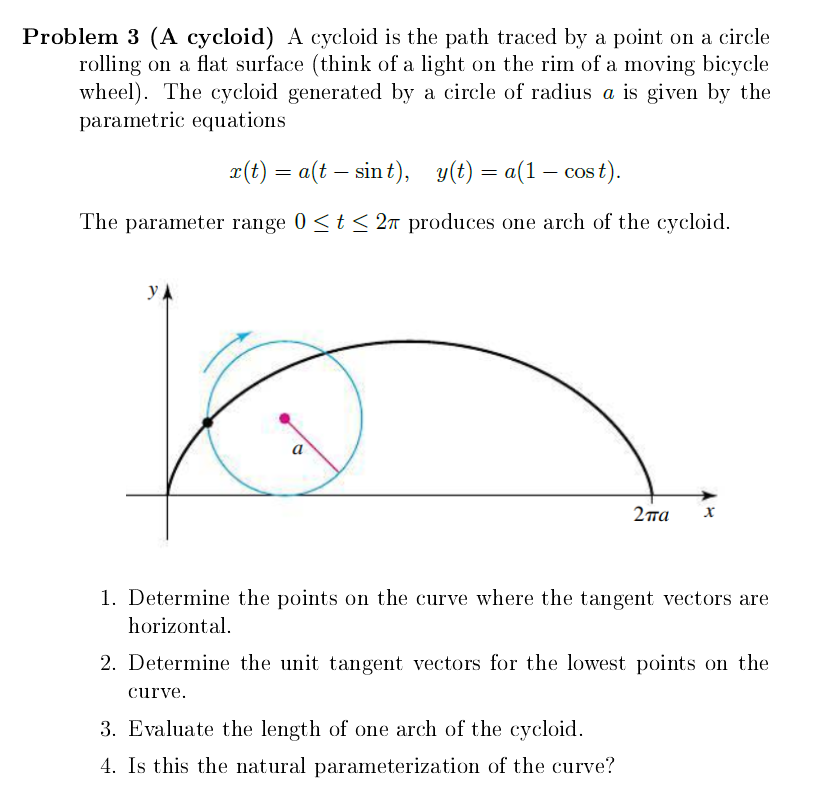
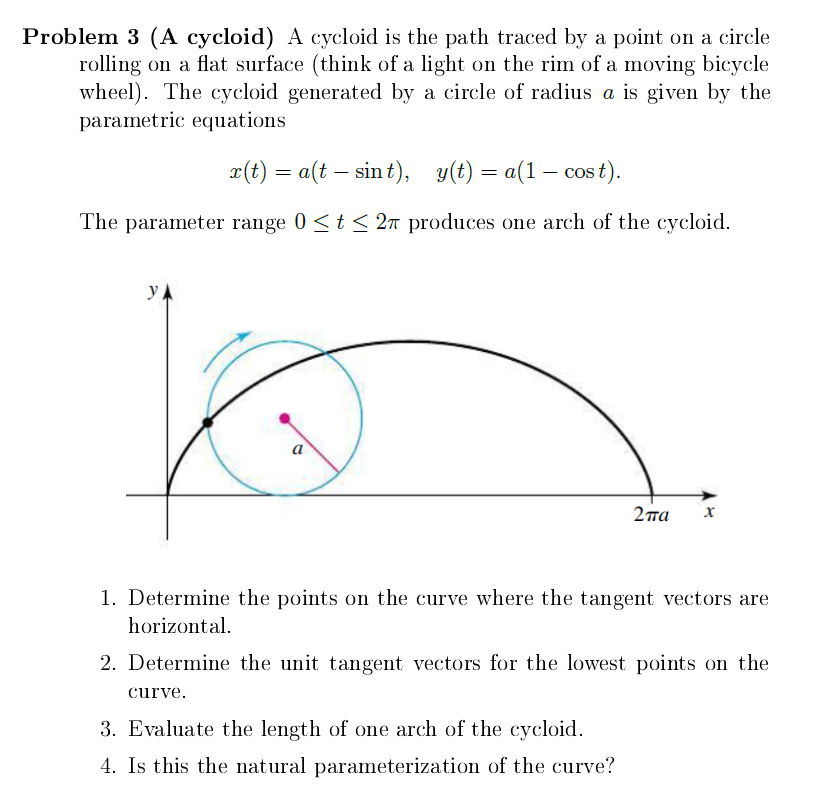
Problern 3 (A cycloid) A cycloid is the path traced by a point on a circle rolling on a at surface (think of a light on the rim of a moving bicycle wheel). The cycloid generated by a circle of radius a is given by the parametric equations 9:05) 2 {1(t sint), t) 2 a(1 cos t). The parameter range 0 g t g 211' produces one arch of the cycloid. 1. Determine the points on the curve where the tangent vectors are horizontal. 2. Determine the unit tangent vectors for the lowest points on the curve. 3. Evaluate the length of one arch of the cycloid. . Is this the natural parameterization of the curve