I am working with a 3d numpy array of size (10, 10, 10). I was wondering if there is a Pythonic way of performing a kernel type (moving window) averaging operation on every point in my 3D numpy array? My data and preliminary code attempt is below. 

I was not sure how to account for grid cells that are located at the edges (boundaries and corners, as they only have a partial of the window kernel around them). For these border cells, I would need weighted average as well. In other words, "for example", for the point located at the index (0, 0, 0) [which does not have a layer above), its resultant point after the kernel weighted averaging operating on it would need to be the weighted average of the available neighboring point from the kernel imposed on it. In this case, when we take the average, to be fair, it should be divided on the available points of its neighbors, and not on the total number of the kernel size (3 * 5 * 5)

 For the weighted_moving_average operation, the 8 immediate surrounding cells (6 points in the same layer as the signal point and two at the layer above & layer below) of the source_point (focal signal point) should have a 70% (stronger weight) whereas the not_immediate surrounding cells (16) in the same layer as the focal signal point should have 30% weights (weaker weights) (as it can be seen in the Weights_of_3D_Kernel elements. 

 import numpy as np

np.random.seed(1)
A = np.random.uniform(size=(10,10, 10))

 

Weights_of_3D_Kernel = np.array([[
       [0.1, 0.1, 0.1, 0.1, 0.1],
       [0.1, 0.3, 0.5, 0.3, 0.1],
       [0.1, 0.5, 0.7, 0.5, 0.1],
       [0.1, 0.3, 0.5, 0.3, 0.1],
       [0.1, 0.1, 0.1, 0.1, 0.1]],

 

      [[0.1, 0.1, 0.1, 0.1, 0.1],
       [0.1, 0.5, 0.7, 0.5, 0.1],
       [0.1, 0.7, 1 , 0.7, 0.1],
       [0.1, 0.5, 0.7, 0.5, 0.1],
       [0.1, 0.1, 0.1, 0.1, 0.1]],

 

      [[0.1, 0.1, 0.1, 0.1, 0.1],
       [0.1, 0.3, 0.5, 0.3, 0.1],
       [0.1, 0.5, 0.7 , 0.5, 0.1],
       [0.1, 0.3, 0.5, 0.3, 0.1],
       [0.1, 0.1, 0.1, 0.1, 0.1]]])

 

 

Transcribed Image Text:

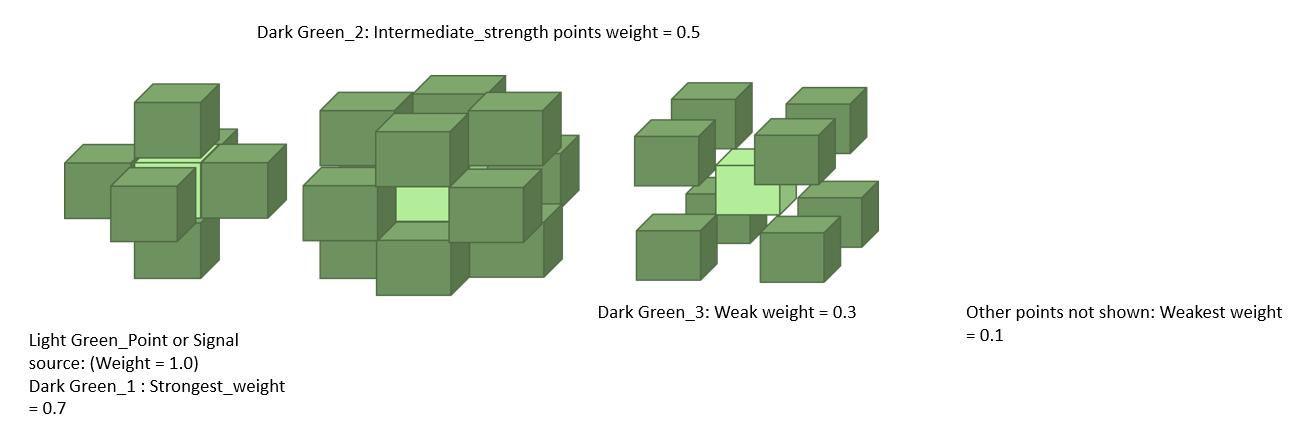
Light Green Point or Signal source: (Weight = 1.0) Dark Green_2: Intermediate_strength points weight = 0.5 Dark Green_1: Strongest_weight = 0.7 Dark Green 3: Weak weight = 0.3 Other points not shown: Weakest weight = 0.1 Light Green Point or Signal source: (Weight = 1.0) Dark Green_2: Intermediate_strength points weight = 0.5 Dark Green_1: Strongest_weight = 0.7 Dark Green 3: Weak weight = 0.3 Other points not shown: Weakest weight = 0.1

Answer rating: 100% (QA)

You can perform the kernelbased weighted moving average operation on your 3D numpy array using ... View the full answer