Question: I claim that merge-sort is actually a linear time algorithm -- i.e., faster than (NlogN). Below is a sketch of my proof that the runtime
I claim that merge-sort is actually a linear time algorithm -- i.e., faster than (NlogN).
Below is a sketch of my proof that the runtime of merge-sort is actually 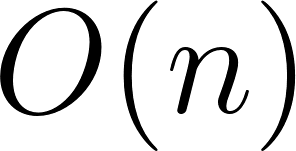 .
.
| For simplicity, I am only proving my claim for powers of 2 (so I don't have to worry about floors and ceilings). We already know that the runtime of merge-sort is described by the recurrence relation
I want to show that |
| BASE-CASE: |
| INDUCTIVE HYPOTHESIS: Assume the claim holds for powers of 2 less than
Notice that this covers |
| Now I have to prove the claim holds at |
| PROOF:
a constant times since we know that "constants don't matter"! Q.E.D. |
Of course, I am wrong! The runtime of MergeSort is really 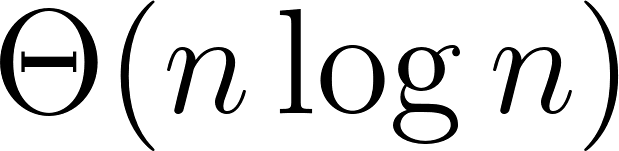 .
.
Your Job: Answer this question:
What is fundamentally wrong with my proof?
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts



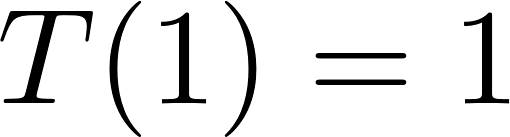
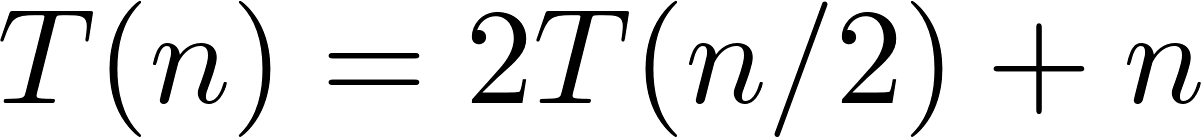 for
for 
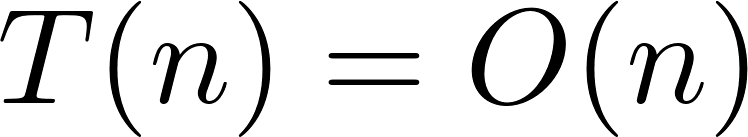 . To make this Big-Oh claim, I will show that that
. To make this Big-Oh claim, I will show that that 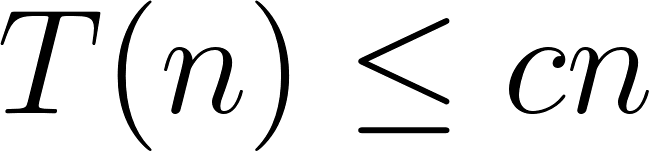 for all
for all  and some constant
and some constant  .
.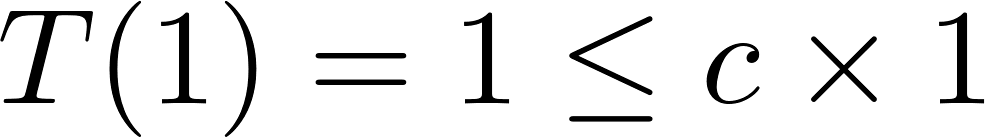 as long as
as long as 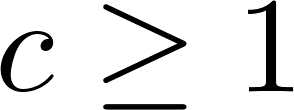 clearly such a constant exists!
clearly such a constant exists!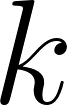 where
where 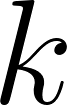 is itself a power of 2:
is itself a power of 2: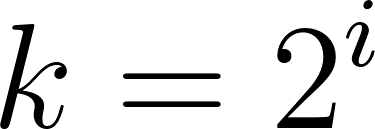 where
where  (and so
(and so 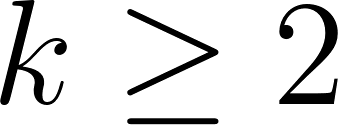 ).
).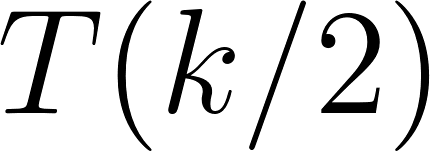
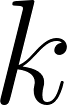 .
.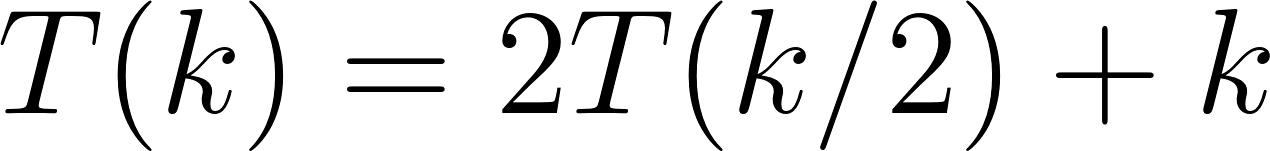 from recurrence relation and
from recurrence relation and 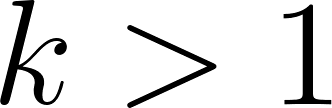
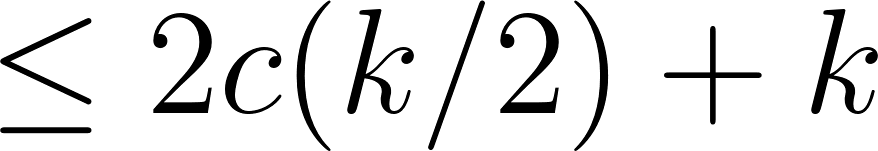 by I.H. applied to
by I.H. applied to 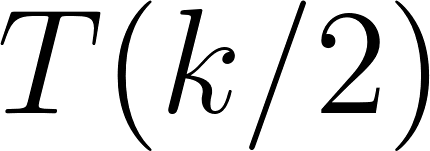
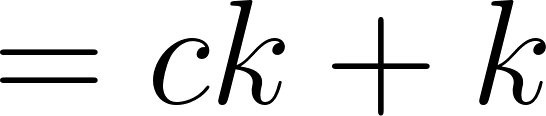 algebra
algebra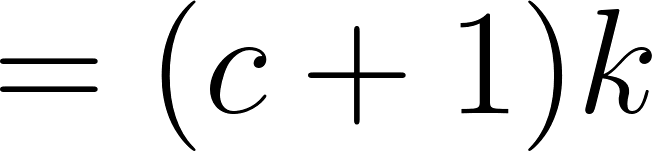 algebra
algebra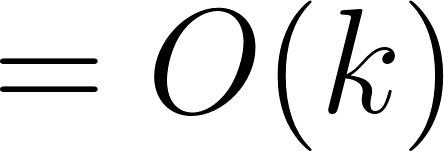 because
because 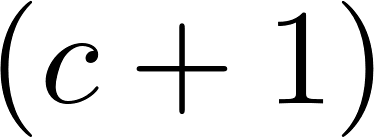 is a constant and
is a constant and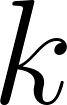 is still
is still 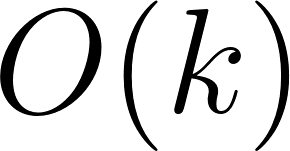 ,
,