I do not get the 1/2/3 steps, please explain

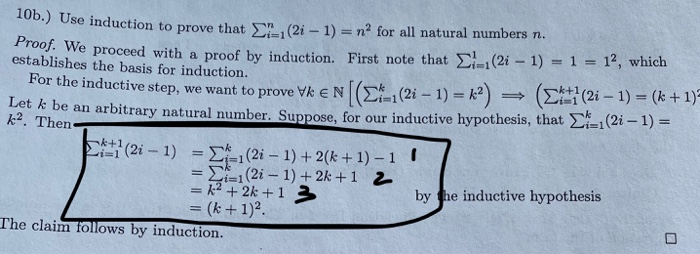
.) Use induction to prove that (2-1) = n2 for all natural numbers n. roof. We proceed with a proof by induction. First note that l (21 - 1) = 1 = 12, which establishes the basis for induction. For the inductive step, we want to prove Vk EN(!_(2i - 1) = R2) = (k+1(21 1) = (k + 1) Let k be an arbitrary natural number. Suppose, for our inductive hypothesis, that -1(21 - 1) = k2. Then L i (2i - 1) = (2i - 1) +2(k+1)-1 = (2-1) + 2k +1 2 = 22 + 2k +1 3 by the inductive hypothesis = (k + 1)2. The claim follows by induction