I do not know how to go about solving this question

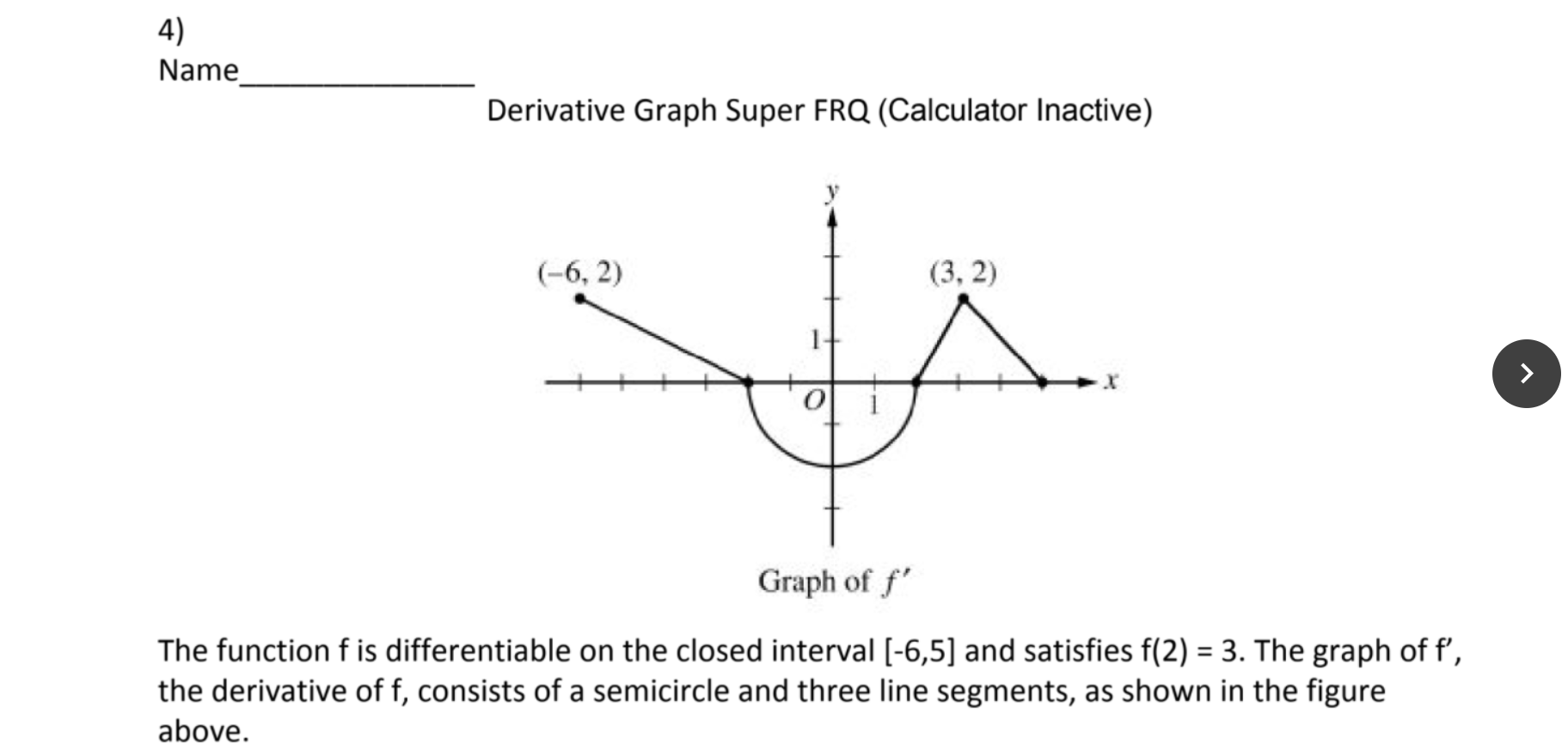
4) Name Derivative Graph Super FRQ (Calculator Inactive) Graph of f ' The function f is differentiable on the closed interval [-6.5] and satisfies f(2) = 3. The graph of f', the derivative of f, consists of a semicircle and three line segments, as shown in the gure above. ape-p: our" arr'Pr'p' Find f(- 6) and f(S). Write an expression for x) that involves an integral. Find f(4) , f(4), and f\" (4) Find all values of x where f is horizontally tangent. Justify. Determine whether a relative minimum, relative maximum, or neither is occurring at those values. Justify your answers. Find the absolute maximum and absolute minimum values of f and the x -values they occur at on the closed interval {-6.5}. On what intervals is f increasing? On what intervals is f decreasing? Justify your answer. On what intervals is f concave up? On what intervals is f concave down? Justify your answer. On what intervals is f decreasing and concave up? Justify your answer. o For what value(s) of x does f have a point of inflection? Justify your answer. Find f( 5), f (0), and f(2). Find each or explain why it does not exist. Let g(x) = x *f(x). Find the equation of the line tangent to the graph of g at x = 2. Let h(x) =f(x) - 2.x. Find all critical values of h(x). . Find the average rate of change of f' on the interval {-6, 5]. There is no point c, on {-6, 5] for which PM is equal to that average rate of change. Explain why this statement does not contradict the Mean Value Theorem. Let p(x) =f(x2 - 1) . Find the slope of the line tangent to the graph of p at the point where x=2