I get all eigenvectors as 0 in (a)...

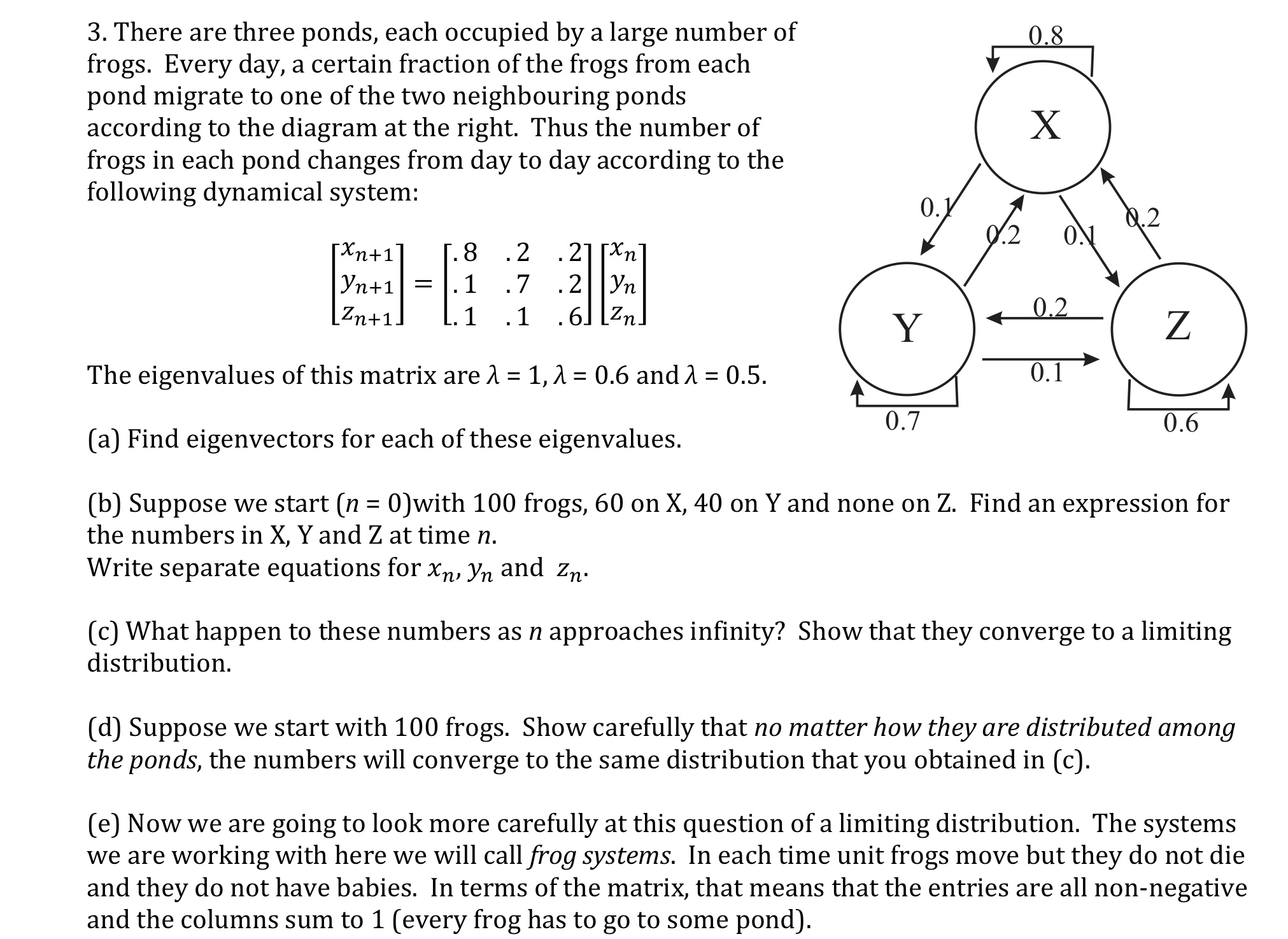
3. There are three ponds, each occupied by a large number of frogs. Every day, a certain fraction of the frogs from each ; l pond migrate to one of the two neighbouring ponds according to the diagram at the right. Thus the number of frogs in each pond changes from day to day according to the following dynamical system: V \\ ' .2 xn+ 1 . xn /4 0\\\\ .8 .2 2 [yn+1] = [.1 .7 .2 yn] Zn+1 .1 .1 .6 Zn 412 > The eigenvalues of this matrix are A = 1, A = 0.6 andA = 0.5. 0.1 l_+ [a] Find eigenvectors for each of these eigenvalues. 0'7 0-6 [b] Suppose we start [n = 0)with 100 frogs, 60 on X, 40 on Y and none on Z. Find an expression for the numbers in X, Y and Z at time n. Write separate equations for xn, yn and zn. [c] What happen to these numbers as n approaches infinity? Show that they converge to a limiting distribution. [d] Suppose we start with 100 frogs. Show carefully that no matter how they are distributed among the ponds, the numbers will converge to the same distribution that you obtained in [c]. [e] Now we are going to look more carefully at this question of a limiting distribution. The systems we are working with here we will call frog systems. In each time unit frogs move but they do not die and they do not have babies. In terms of the matrix, that means that the entries are all non-negative and the columns sum to 1 [every frog has to go to some pond]