I have 3 questions, based on the attachment below:

1. Explain how the term underlined by BLUE is obtained
2. Does the statement underlined by RED, refer to the statement "but that these partials are not continuous at (0,0)". Please explain in more detail
3. Please explain in detail, the GREEN box

Please explain clearly showing each step as thoroughly as possible.

If you are using hand-written notes, then please ensure they are tidy and legible as untidy written notes are difficult to interpret.

Alternatively use LaTeX.

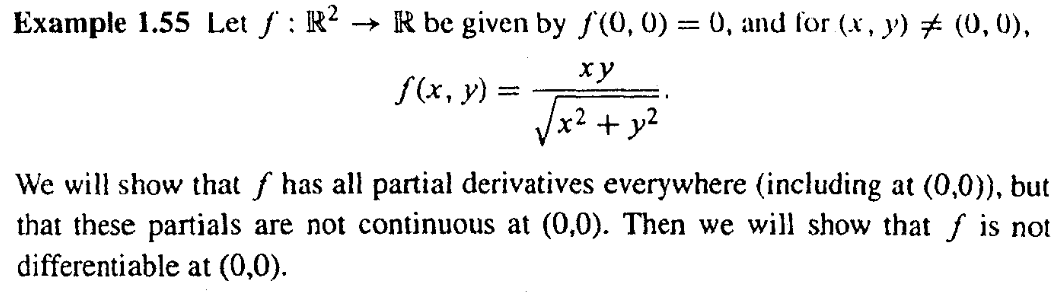
Example 1.55 Let f : Iz - R be given by f (0, 0) = 0, and for (x, y) # (0, 0), xy f (x, y) = Vx2 + 1/2 We will show that f has all partial derivatives everywhere (including at (0,0)), but that these partials are not continuous at (0,0). Then we will show that f is not differentiable at (0,0).Since f(x, 0) = 0 for any x / 0; it-is immediate that for all x # 0, - (x, 0) = lim J( x. y) - f(x, 0) X = lim = 1. x 2 + 12 Similarly, at all points of the form (0, y) for y # 0, we have af(0, y)/ax = 1. However, note that of (0, 0) = lim f(x. 0) - f(0, 0) 0-0 = lim == 0, ax * -+ 0 X x-+0 X so af (0, 0) /3x exists at (0, 0), but is not the limit of af (0, y) /ax as y - O. Similarly. we also have a f(0, 0) /ay = 0 # 1 = limx -.oaf (x, 0) /ay. Suppose f . ere differentiable at (0, 0). Then, the derivative Df (0, 0) must coin- cide with the vector of partials at (0,0) so we must have DS (0, 0) = (0, 0). However. from the definition of the derivative, we must also have lim II f (x. y) - f(0.0) - Df (0. 0) . (x. v)Il = 0. (x. y)- (0.0) I(x, y) - (0, 0) 11 but this is impossible if Df (0, 0) = 0. To see this, take any point (x, y) of the form (a, a) for some a > 0, and note that every neighborhood of (0,0) contains at least one such point. Since f(0, 0) = 0, Df(0, 0) = (0, 0), and II (x. y)ll = Vx2 + )2. it follows that ll f(a, a) - f(0, 0) - Df(0, 0) . (a, a)ll a2 = NI . Il (a, a) - (0, 0) 11 202 so the limit of this fraction as a - 0 cannot be zero