I have answer to question 1 but I need answer to question number 2.

2. Find a representation for this series in terms of the sums of a sequence, and use convergence tests to determine whether or not this series will converge. If it converges, give the area to which the series will converge.

we need to find sums of the sequence and find out if it converges or not. Attachments are below please help me out. Please please please please

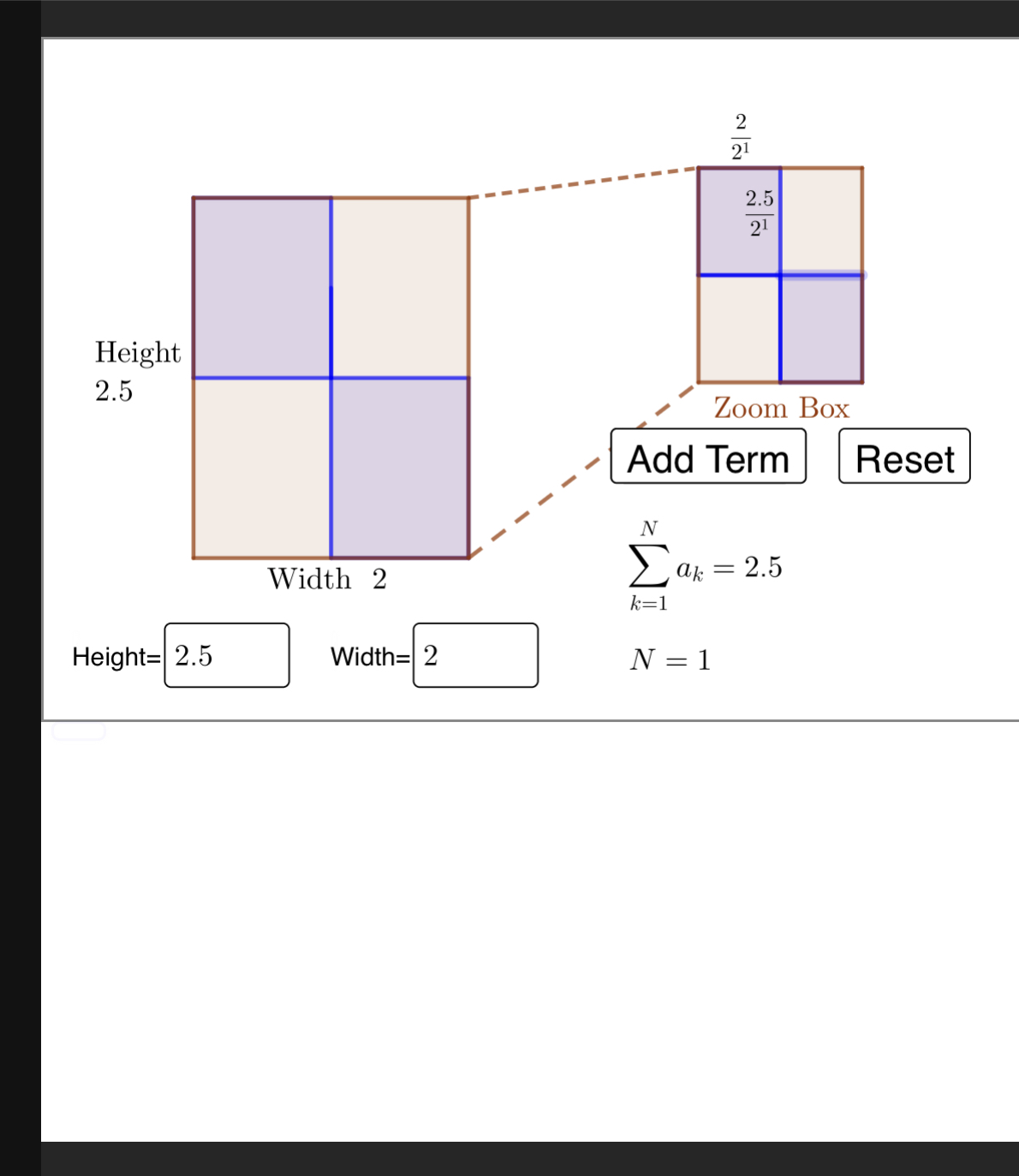
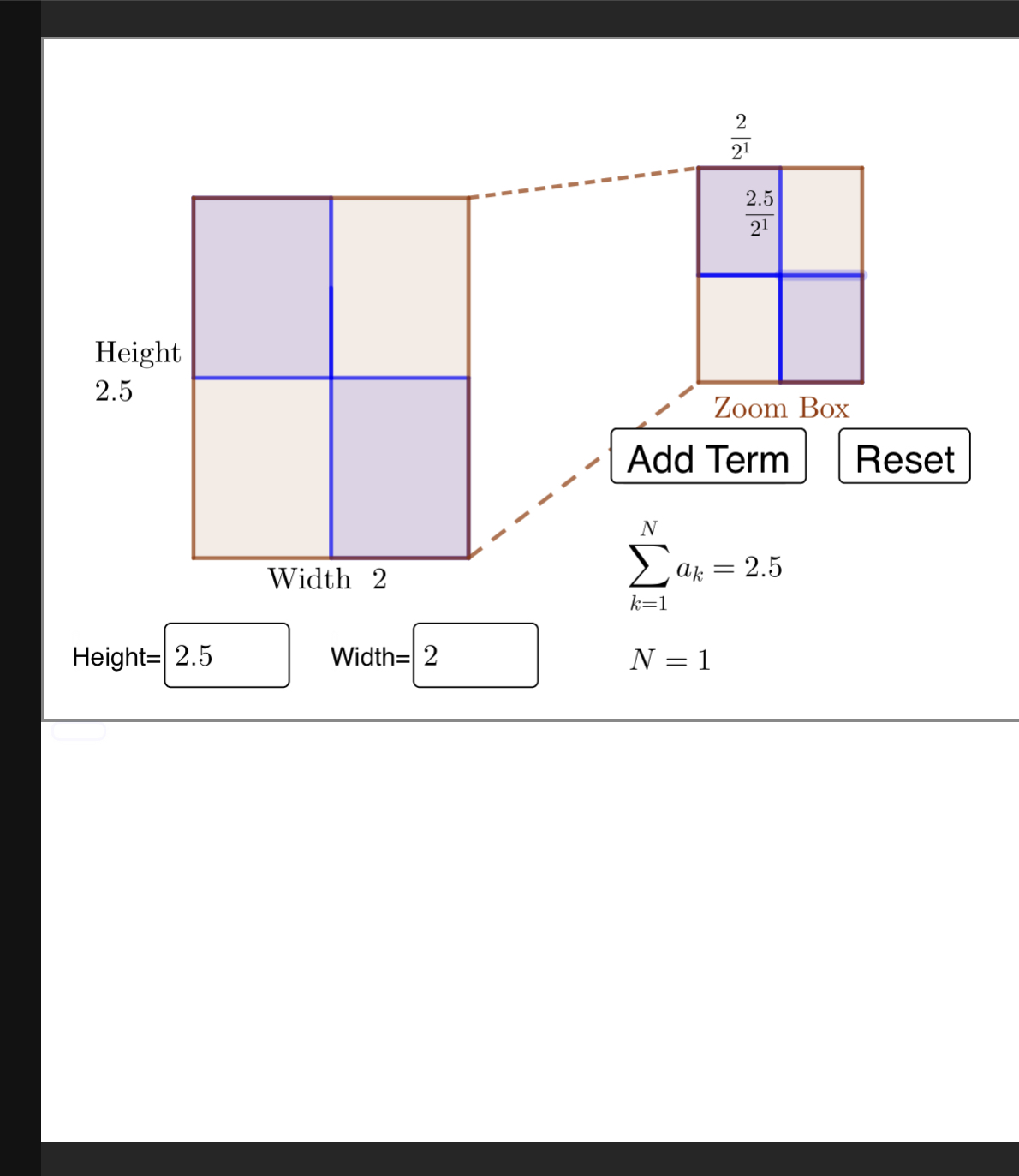
Generate New Values You may enter the randomly generated height and width values into the input boxes in the bottom left corner of the applet. The applet is depicting the partial sums of an innite series. The terms in the innite series ll in the new rectangles shown in the "Zoom Box", and in the globally viewed rectangle as well. You may click the "Add Term" button to see the total area represented by the next term in the innite series. You may click "Reset" to start at N=O. After two new terms, you may click "Zoom in" to move the zoom box forward. This allows you to see how the terms progress even if the areas are quite small. Notice that the zoom box moves to cover a smaller region on the left global rectangle. Argue whether this series converges or not in the fol lowing ways: 1. Argue geometrically by talking about over and underestimates of the unknown value of the innite series. As the terms of the series add area to the visualized object, argue whether or not it is possible to give both over and underestimates of the total area being formed by series, and whether or not it is possible to always reduce the error between the over and underestimates of the area being constructed. If it converges, give the area to which the series will converge. . Find a representation for this series in terms of the sums of a sequence, and use convergence tests to determine whether or not this series will converge. If it converges, give the area to which the series will converge.